"עשרונים. פעולות על עשרונים" (שיעור הכללה). עשרוניים, הגדרות, סימון, דוגמאות, פעולות עם עשרונים

כאשר מוסיפים שברים עשרוניים, יש צורך לכתוב אותם אחד מתחת לשני כך שאותן ספרות יהיו זו מתחת לשנייה, והפסיק נמצא מתחת לפסיק, ולהוסיף את השברים כמו שמוסיפים מספרים טבעיים. בוא נוסיף, למשל, את השברים 12.7 ו-3.442. השבר הראשון מכיל ספרה אחת אחרי הנקודה העשרונית, והשני מכיל שלוש. כדי לבצע חיבור, נמיר את השבר הראשון כך שיהיו שלוש ספרות אחרי הנקודה העשרונית: , ואז

מספרים עשרוניים מופחתים באותו אופן. מצא את ההבדל בין המספרים 13.1 ו-0.37:

כאשר מכפילים שברים עשרוניים, מספיק להכפיל את המספרים הנתונים, תוך התעלמות מהפסיקים (כמספרים טבעיים), ולאחר מכן, כתוצאה מכך, להפריד כמה ספרות עם פסיק מימין כפי שיש אחרי הנקודה העשרונית בשני הגורמים. בסך הכל.

לדוגמה, בוא נכפיל את 2.7 ב-1.3. יש לנו . הפרד שתי ספרות מימין בפסיק (סכום הספרות של הגורמים אחרי הנקודה העשרונית שווה לשניים). כתוצאה מכך, נקבל 2.7 1.3 = 3.51.

אם יש פחות ספרות במוצר ממה שצריך להפריד בפסיק, אז האפסים החסרים נכתבים מלפנים, למשל:

שקול להכפיל שבר עשרוני ב-10, 100, 1000 וכו'. יהיה צורך להכפיל את השבר 12.733 ב-10. יש לנו . אם נפריד שלוש ספרות בצד ימין עם פסיק, נקבל אבל. אומר,

12,733 10=127.33. לפיכך, הכפלת שבר עשרוני ב- Yu מצטמצמת להזזת הנקודה העשרונית ספרה אחת ימינה.

באופן כללי, על מנת להכפיל שבר עשרוני ב-10, 100, 1000, יש צורך להזיז את הפסיק בשבר זה ב-1, 2, 3 ספרות ימינה. הקצאת, במידת הצורך, מספר מסוים של אפסים ל- שבר מימין). לדוגמה,

החלוקה של שבר עשרוני במספר טבעי מתבצעת באותו אופן כמו החלוקה של מספר טבעי במספר טבעי, ופסיק ממוקם במנה לאחר השלמת חלוקת החלק השלם. בואו נחלק את 22.1 ב-13:

אם החלק השלם של הדיבידנד פחות מחלק, אז התשובה היא אפס מספרים שלמים, לדוגמה:

שקול כעת את החלוקה של עשרוני בעשרוני. נניח שעלינו לחלק את 2.576 ב-1.12. לשם כך, הן בדיווידנד והן במחלק, נעביר את הפסיק ימינה במספר ספרות שיש אחרי הנקודה העשרונית במחלק (בדוגמה זו, שתיים). במילים אחרות, הכפל את הדיבידנד והמחלק ב-100 - זה לא ישנה את המנה. אז אתה צריך לחלק את השבר 257.6 במספר הטבעי 112, כלומר הבעיה מצטמצמת למקרה שכבר נחשב:

כדי לחלק שבר עשרוני לתוכו יש צורך להעביר את הפסיק לספרות שמאלה בשבר זה (במקרה זה, במידת הצורך, המספר הנדרש של אפסים מוקצה לשמאל). לדוגמה, .

כשם שחלוקה לא תמיד אפשרית עבור מספרים טבעיים, כך היא לא תמיד אפשרית עבור שברים עשרוניים. חלקו למשל 2.8 ב-0.09:

התוצאה היא מה שנקרא שבר עשרוני אינסופי. במקרים כאלה, עבור לשברים רגילים. לדוגמה:

ייתכן שיתברר שמספרים מסוימים נכתבים בצורה של שברים רגילים, אחרים - בצורה של מספרים מעורבים, ואחרים - בצורה של שברים עשרוניים. כאשר מבצעים פעולות במספרים כאלה, אתה יכול לעשות דברים שונים: או להפוך עשרונים לשברים רגילים ולהחיל את הכללים לפעולות על שברים רגילים, או להמיר שברים רגילים ומספרים מעורבים לשברים עשרוניים (אם אפשר) ולהחיל את הכללים לפעולות על שברים רגילים. שברים עשרוניים.

במדריך זה, נסתכל על כל אחת מהפעולות הללו אחת לאחת.

תוכן השיעור

הוספת עשרונים

כידוע, לעשרוני יש חלק שלם וחלק חלקי. בעת הוספת עשרונים, החלקים השלמים והשברים מתווספים בנפרד.

לדוגמה, בואו נוסיף את העשרוניות 3.2 ו-5.3. נוח יותר להוסיף שברים עשרוניים בעמודה.

ראשית, אנו כותבים את שני השברים הללו בטור, בעוד שהחלקים השלמים חייבים להיות מתחת לחלקים השלמים, והשברים מתחת לשברים. בבית הספר, דרישה זו נקראת "פסיק מתחת לפסיק".

בוא נכתוב את השברים בעמודה כך שהפסיק יהיה מתחת לפסיק:

אנו מתחילים להוסיף את החלקים השברים: 2 + 3 \u003d 5. אנו רושמים את החמישה בחלק השבר של התשובה שלנו:

כעת נחבר את החלקים השלמים: 3 + 5 = 8. נכתוב את השמונה בחלק השלם של התשובה שלנו:

כעת אנו מפרידים את החלק השלם מהחלק השברי באמצעות פסיק. כדי לעשות זאת, אנו שוב פועלים לפי הכלל "פסיק מתחת לפסיק":

קיבלתי את התשובה 8.5. אז הביטוי 3.2 + 5.3 שווה ל-8.5

למעשה, לא הכל פשוט כמו שזה נראה במבט ראשון. גם כאן יש מלכודות, עליהם נדבר כעת.

מקומות בעשרונים

לעשרונים, כמו למספרים רגילים, יש ספרות משלהם. אלו מקומות עשיריים, מקומות מאה, מקומות אלף. במקרה זה, הספרות מתחילות אחרי הנקודה העשרונית.

הספרה הראשונה אחרי הנקודה העשרונית אחראית למקום העשיריות, הספרה השנייה אחרי הנקודה העשרונית למקום המאיות, הספרה השלישית אחרי הנקודה העשרונית למקום האלפיות.

הספרות בשברים עשרוניים מאחסנות חלק מידע שימושי. בפרט, הם מדווחים כמה עשיריות, מאיות ואלפיות הן בעשרוניות.

לדוגמה, שקול את העשרוני 0.345

המיקום שבו ממוקם המשולש נקרא מקום עשירי

המיקום שבו ממוקמים הארבע נקרא מקום מאיות

המיקום שבו נמצא החמישה נקרא אלפיות

בואו נסתכל על הנתון הזה. אנו רואים שבקטגוריית העשיריות יש שלשה. זה מצביע על כך שיש שלוש עשיריות בשבר העשרוני 0.345.

אם נוסיף את השברים, ואז נקבל את השבר העשרוני המקורי 0.345

ניתן לראות שבהתחלה קיבלנו את התשובה, אבל המרנו אותה לשבר עשרוני וקיבלנו 0.345.

כאשר מוסיפים שברים עשרוניים, פועלים לפי אותם עקרונות וכללים כמו בהוספת מספרים רגילים. הוספת שברים עשרוניים מתרחשת לפי ספרות: עשיריות מתווספות לעשיריות, מאיות עד מאיות, אלפיות לאלף.

לכן, כאשר מוסיפים שברים עשרוניים, יש צורך לפעול לפי הכלל "פסיק מתחת לפסיק". פסיק מתחת לפסיק מספק את אותו סדר שבו העשיריות מתווספות לעשיריות, מאיות עד מאיות, אלפיות לאלף.

דוגמה 1מצא את הערך של הביטוי 1.5 + 3.4

קודם כל, נוסיף את החלקים השברים 5 + 4 = 9. נכתוב את התשע בחלק השבר של התשובה שלנו:

כעת נחבר את החלקים השלמים 1 + 3 = 4. נכתוב את הארבעה בחלק השלם של התשובה שלנו:

כעת אנו מפרידים את החלק השלם מהחלק השברי באמצעות פסיק. לשם כך, אנו מקפידים שוב על הכלל "פסיק תחת פסיק":

קיבלתי את התשובה 4.9. אז הערך של הביטוי 1.5 + 3.4 הוא 4.9

דוגמה 2מצא את הערך של הביטוי: 3.51 + 1.22

אנו כותבים את הביטוי הזה בעמודה, תוך הקפדה על הכלל "פסיק מתחת לפסיק"

קודם כל, הוסף את החלק השברי, כלומר מאיות 1+2=3. אנו כותבים את המשולש בחלק המאה של התשובה שלנו:

כעת הוסף עשיריות מ-5+2=7. אנו רושמים את השבעה בחלק העשירי של תשובתנו:

כעת הוסף את החלקים השלמים 3+1=4. אנו רושמים את הארבעה בכל החלק של התשובה שלנו:

אנו מפרידים את החלק השלם מהחלק השברי באמצעות פסיק, תוך התבוננות בכלל "פסיק מתחת לפסיק":

קיבלתי את התשובה 4.73. אז הערך של הביטוי 3.51 + 1.22 הוא 4.73

3,51 + 1,22 = 4,73

כמו במספרים רגילים, כאשר מוסיפים שברים עשרוניים, . במקרה זה, ספרה אחת כתובה בתשובה, והשאר מועברים לספרה הבאה.

דוגמה 3מצא את הערך של הביטוי 2.65 + 3.27

אנו כותבים את הביטוי הזה בטור:

הוסף מאיות של 5+7=12. המספר 12 לא יתאים בחלק המאה של התשובה שלנו. לכן, בחלק המאה, אנו כותבים את המספר 2, ומעבירים את היחידה לביט הבא:

כעת נוסיף את העשיריות של 6+2=8 בתוספת היחידה שקיבלנו מהפעולה הקודמת, נקבל 9. נכתוב את המספר 9 בעשירית של התשובה שלנו:

כעת הוסף את החלקים השלמים 2+3=5. אנו כותבים את המספר 5 בחלק השלם של התשובה שלנו:

קיבלתי את התשובה 5.92. אז הערך של הביטוי 2.65 + 3.27 הוא 5.92

2,65 + 3,27 = 5,92

דוגמה 4מצא את הערך של הביטוי 9.5 + 2.8

כתוב את הביטוי הזה בעמודה

נוסיף את החלקים השברים 5 + 8 = 13. המספר 13 לא יתאים בחלק השבר של התשובה שלנו, אז קודם כל רושמים את המספר 3, ומעבירים את היחידה לספרה הבאה, או יותר נכון מעבירים אותה למספר השלם חֵלֶק:

כעת נוסיף את החלקים השלמים 9+2=11 בתוספת היחידה שקיבלנו מהפעולה הקודמת, נקבל 12. נכתוב את המספר 12 בחלק השלם של התשובה שלנו:

הפרד את החלק השלם מהחלק השברי באמצעות פסיק:

קיבלתי את התשובה 12.3. אז הערך של הביטוי 9.5 + 2.8 הוא 12.3

9,5 + 2,8 = 12,3

בעת הוספת שברים עשרוניים, מספר הספרות אחרי הנקודה העשרונית בשני השברים חייב להיות זהה. אם אין מספיק ספרות, אז המקומות האלה בחלק השברי מלאים באפסים.

דוגמה 5. מצא את הערך של הביטוי: 12.725 + 1.7

לפני כתיבת ביטוי זה בעמודה, הבה נהפוך את מספר הספרות לאחר הנקודה העשרונית בשני השברים זהה. לשבר העשרוני 12.725 יש שלוש ספרות אחרי הנקודה העשרונית, ואילו לשבר 1.7 יש רק אחת. אז בשבר 1.7 בסוף צריך להוסיף שני אפסים. אז נקבל את השבר 1,700. עכשיו אתה יכול לכתוב את הביטוי הזה בעמודה ולהתחיל לחשב:

הוסף אלפיות מ-5+0=5. אנו כותבים את המספר 5 בחלק האלף של התשובה שלנו:

הוסף מאיות של 2+0=2. אנו כותבים את המספר 2 בחלק המאה של התשובה שלנו:

הוסף עשיריות מ-7+7=14. המספר 14 לא יתאים לעשירית מהתשובה שלנו. לכן, קודם כל רושמים את המספר 4 ומעבירים את היחידה לסיביות הבאה:

כעת נוסיף את החלקים השלמים 12+1=13 בתוספת היחידה שקיבלנו מהפעולה הקודמת, נקבל 14. נכתוב את המספר 14 בחלק השלם של התשובה שלנו:

הפרד את החלק השלם מהחלק השברי באמצעות פסיק:

קיבלתי את התשובה 14,425. אז הערך של הביטוי 12.725+1.700 הוא 14.425

12,725+ 1,700 = 14,425

חיסור של עשרונים

בעת הפחתת שברים עשרוניים, עליך לפעול לפי אותם כללים כמו בעת הוספה: "פסיק מתחת לפסיק" ו"מספר שווה של ספרות אחרי נקודה עשרונית".

דוגמה 1מצא את הערך של הביטוי 2.5 - 2.2

אנו כותבים את הביטוי הזה בעמודה, תוך הקפדה על כלל "פסיק בפסיק":

אנו מחשבים את החלק השברי 5−2=3. אנו כותבים את המספר 3 בחלק העשירי של התשובה שלנו:

חשב את החלק השלם 2−2=0. אנו כותבים אפס בחלק השלם של התשובה שלנו:

הפרד את החלק השלם מהחלק השברי באמצעות פסיק:

קיבלנו את התשובה 0.3. אז הערך של הביטוי 2.5 - 2.2 שווה ל-0.3

2,5 − 2,2 = 0,3

דוגמה 2מצא את הערך של הביטוי 7.353 - 3.1

בביטוי הזה כמות שונהספרות אחרי הנקודה העשרונית. בשבר 7.353 יש שלוש ספרות אחרי הנקודה העשרונית, ובשבר 3.1 יש רק אחת. המשמעות היא שבשבר 3.1 יש להוסיף שני אפסים בסוף כדי להפוך את מספר הספרות בשני השברים זהה. אז נקבל 3,100.

עכשיו אתה יכול לכתוב את הביטוי הזה בעמודה ולחשב אותו:

קיבלתי את התשובה 4,253. אז הערך של הביטוי 7.353 - 3.1 הוא 4.253

7,353 — 3,1 = 4,253

כמו במספרים רגילים, לפעמים תצטרך לשאול אחד מהסיביות הסמוכה אם חיסור הופך לבלתי אפשרי.

דוגמה 3מצא את הערך של הביטוי 3.46 - 2.39

הורידו מאיות מ-6-9. מהמספר 6 אין להחסיר את המספר 9. לכן, אתה צריך לקחת יחידה מהספרה הסמוכה. לאחר ששאלתי אחד מהספרה השכנה, המספר 6 הופך למספר 16. כעת נוכל לחשב את המאיות של 16−9=7. אנו רושמים את השבעה בחלק המאה של התשובה שלנו:

כעת הפחיתו עשיריות. מכיוון שלקחנו יחידה אחת בקטגוריית העשיריות, הנתון שהיה ממוקם שם ירד ביחידה אחת. במילים אחרות, המקום העשירי הוא כעת לא המספר 4, אלא המספר 3. בוא נחשב את העשיריות של 3−3=0. אנו כותבים אפס בחלק העשירי של התשובה שלנו:

כעת נחסר את החלקים השלמים 3−2=1. אנו כותבים את היחידה בחלק השלם של התשובה שלנו:

הפרד את החלק השלם מהחלק השברי באמצעות פסיק:

קיבלתי את התשובה 1.07. אז הערך של הביטוי 3.46-2.39 שווה ל-1.07

3,46−2,39=1,07

דוגמה 4. מצא את הערך של הביטוי 3−1.2

דוגמה זו מפחיתה עשרוני ממספר שלם. בוא נכתוב את הביטוי הזה בעמודה כך שהחלק השלם של השבר העשרוני 1.23 נמצא מתחת למספר 3

כעת נהפוך את מספר הספרות לאחר הנקודה העשרונית להיות זהה. לשם כך, לאחר המספר 3, שים פסיק והוסף אפס אחד:

כעת נחסר עשיריות: 0-2. אין להחסיר את המספר 2 מאפס. לכן, אתה צריך לקחת יחידה מהספרה הסמוכה. בהשאלה אחת מהספרה הסמוכה, 0 הופך למספר 10. כעת ניתן לחשב את העשיריות של 10−2=8. אנו רושמים את השמונה בחלק העשירי של התשובה שלנו:

כעת הפחיתו את החלקים השלמים. בעבר, המספר 3 היה ממוקם במספר השלם, אבל השאלנו ממנו יחידה אחת. כתוצאה מכך, הוא הפך למספר 2. לכן, נחסר 1 מ-2. 2−1=1. אנו כותבים את היחידה בחלק השלם של התשובה שלנו:

הפרד את החלק השלם מהחלק השברי באמצעות פסיק:

קיבלתי את התשובה 1.8. אז הערך של הביטוי 3−1.2 הוא 1.8

כפל עשרוני

הכפלת ספרות עשרוניות היא קלה ואפילו מהנה. כדי להכפיל עשרוניות, עליך להכפיל אותם כמו מספרים רגילים, תוך התעלמות מהפסיקים.

לאחר קבלת התשובה, יש צורך להפריד את החלק השלם מהחלק השברי באמצעות פסיק. לשם כך, עליך לספור את מספר הספרות לאחר הנקודה העשרונית בשני השברים, ולאחר מכן לספור את אותו מספר הספרות מימין בתשובה ולשים פסיק.

דוגמה 1מצא את הערך של הביטוי 2.5 × 1.5

אנו מכפילים את השברים העשרוניים הללו כמספרים רגילים, תוך התעלמות מהפסיקים. כדי להתעלם מהפסיקים, אתה יכול לדמיין זמנית שהם נעדרים לחלוטין:

קיבלנו 375. במספר זה, יש צורך להפריד את כל החלק מהחלק השבר עם פסיק. כדי לעשות זאת, עליך לספור את מספר הספרות לאחר הנקודה העשרונית בשברים של 2.5 ו-1.5. בשבר הראשון יש ספרה אחת אחרי הנקודה העשרונית, בשבר השני יש גם אחת. בסך הכל שני מספרים.

אנחנו חוזרים למספר 375 ומתחילים לנוע מימין לשמאל. עלינו לספור שתי ספרות מימין ולשים פסיק:

קיבלתי את התשובה 3.75. אז הערך של הביטוי 2.5 × 1.5 הוא 3.75

2.5 x 1.5 = 3.75

דוגמה 2מצא את הערך של הביטוי 12.85 × 2.7

בואו נכפיל את העשרוניות האלה, תוך התעלמות מהפסיקים:

יש לנו 34695. במספר זה, אתה צריך להפריד את החלק השלם מהחלק השבר עם פסיק. כדי לעשות זאת, עליך לחשב את מספר הספרות לאחר הנקודה העשרונית בשברים של 12.85 ו- 2.7. בשבר 12.85 יש שתי ספרות אחרי הנקודה העשרונית, בשבר 2.7 יש ספרה אחת - בסך הכל שלוש ספרות.

אנחנו חוזרים למספר 34695 ומתחילים לנוע מימין לשמאל. עלינו לספור שלוש ספרות מימין ולשים פסיק:

קיבלתי את התשובה 34,695. אז הערך של הביטוי 12.85 × 2.7 הוא 34.695

12.85 x 2.7 = 34.695

הכפלת עשרוני במספר רגיל

לפעמים יש מצבים שבהם אתה צריך להכפיל עשרוני ב מספר נפוץ.

כדי להכפיל מספר עשרוני ומספר רגיל, עליך להכפיל אותם, ללא קשר לפסיק בעשרוני. לאחר קבלת התשובה, יש צורך להפריד את החלק השלם מהחלק השברי באמצעות פסיק. כדי לעשות זאת, עליך לספור את מספר הספרות אחרי הנקודה העשרונית בשבר העשרוני, ולאחר מכן בתשובה, לספור את אותו מספר ספרות ימינה ולשים פסיק.

לדוגמה, הכפל 2.54 ב-2

נכפיל את השבר העשרוני 2.54 במספר הרגיל 2, תוך התעלמות מהפסיק:

קיבלנו את המספר 508. במספר זה, אתה צריך להפריד את החלק השלם מהחלק השבר עם פסיק. לשם כך, עליך לספור את מספר הספרות לאחר הנקודה העשרונית בשבר 2.54. לשבר 2.54 יש שתי ספרות אחרי הנקודה העשרונית.

אנחנו חוזרים למספר 508 ומתחילים לנוע מימין לשמאל. עלינו לספור שתי ספרות מימין ולשים פסיק:

קיבלתי את התשובה 5.08. אז הערך של הביטוי 2.54 × 2 הוא 5.08

2.54 x 2 = 5.08

הכפלת מספרים עשרוניים ב-10, 100, 1000

הכפלת מספרים עשרוניים ב-10, 100 או 1000 מתבצעת באותו אופן כמו הכפלת עשרונים במספרים רגילים. יש צורך לבצע את הכפל, תוך התעלמות מהפסיק בשבר העשרוני, ואז בתשובה להפריד את החלק השלם מהחלק השבר, לספור את אותו מספר ספרות בצד ימין כפי שהיו ספרות אחרי הנקודה העשרונית. שבריר.

לדוגמה, הכפל 2.88 ב-10

בוא נכפיל את השבר העשרוני 2.88 ב-10, תוך התעלמות מהפסיק בשבר העשרוני:

קיבלנו 2880. במספר זה, אתה צריך להפריד את כל החלק מהחלק השבר עם פסיק. כדי לעשות זאת, עליך לספור את מספר הספרות לאחר הנקודה העשרונית בשבר 2.88. אנו רואים שבשבר 2.88 יש שתי ספרות אחרי הנקודה העשרונית.

אנחנו חוזרים למספר 2880 ומתחילים לנוע מימין לשמאל. עלינו לספור שתי ספרות מימין ולשים פסיק:

קיבלתי את התשובה 28.80. נזרוק את האפס האחרון - נקבל 28.8. אז הערך של הביטוי 2.88 × 10 הוא 28.8

2.88 x 10 = 28.8

יש דרך שנייה להכפיל שברים עשרוניים ב-10, 100, 1000. שיטה זו הרבה יותר פשוטה ונוחה. הוא מורכב מהעובדה שהפסיק בשבר העשרוני זז ימינה במספר ספרות כמו שיש אפסים במכפיל.

לדוגמה, בואו נפתור את הדוגמה הקודמת 2.88×10 בצורה זו. מבלי לתת חישובים, אנו מיד מסתכלים על הפקטור 10. אנו מתעניינים בכמה אפסים יש בו. אנו רואים שיש לו אפס אחד. כעת בשבר 2.88 נעביר את הנקודה העשרונית ימינה בספרה אחת, נקבל 28.8.

2.88 x 10 = 28.8

בואו ננסה להכפיל את 2.88 ב-100. מיד נסתכל על הפקטור 100. מעניין אותנו כמה אפסים יש בו. אנו רואים שיש לו שני אפסים. כעת בשבר 2.88 נעביר את הנקודה העשרונית ימינה בשתי ספרות, נקבל 288

2.88 x 100 = 288

בואו ננסה להכפיל את 2.88 ב-1000. מיד נסתכל על הפקטור 1000. מעניין אותנו כמה אפסים יש בו. אנו רואים שיש לו שלושה אפסים. כעת בשבר 2.88 נעביר את הנקודה העשרונית ימינה בשלוש ספרות. הספרה השלישית אינה שם, אז נוסיף עוד אפס. כתוצאה מכך, אנו מקבלים 2880.

2.88 x 1000 = 2880

הכפלת מספרים עשרוניים ב-0.1 0.01 ו-0.001

הכפלת עשרונים ב-0.1, 0.01 ו-0.001 פועלת באותו אופן כמו הכפלת עשרוני בעשרוני. יש צורך להכפיל שברים כמו מספרים רגילים, ולשים פסיק בתשובה, לספור כמה ספרות בצד ימין כמו שיש ספרות אחרי הנקודה העשרונית בשני השברים.

לדוגמה, הכפל 3.25 ב-0.1

אנחנו מכפילים את השברים האלה כמו מספרים רגילים, תוך התעלמות מהפסיקים:

קיבלנו 325. במספר הזה, אתה צריך להפריד את כל החלק מהחלק השבר עם פסיק. לשם כך, עליך לחשב את מספר הספרות לאחר הנקודה העשרונית בשברים של 3.25 ו-0.1. בשבר 3.25 יש שתי ספרות אחרי הנקודה העשרונית, בשבר 0.1 יש ספרה אחת. בסך הכל שלושה מספרים.

אנחנו חוזרים למספר 325 ומתחילים לנוע מימין לשמאל. אנחנו צריכים לספור שלוש ספרות בצד ימין ולשים פסיק. לאחר ספירת שלוש ספרות, אנו מגלים שהמספרים נגמרו. במקרה זה, עליך להוסיף אפס אחד ולשים פסיק:

קיבלנו את התשובה 0.325. אז הערך של הביטוי 3.25 × 0.1 הוא 0.325

3.25 x 0.1 = 0.325

ישנה דרך שנייה להכפיל עשרוניות ב-0.1, 0.01 ו-0.001. שיטה זו הרבה יותר קלה ונוחה. זה מורכב מהעובדה שהפסיק בשבר העשרוני זז שמאלה במספר ספרות כמו שיש אפסים במכפיל.

לדוגמה, בואו נפתור את הדוגמה הקודמת 3.25 × 0.1 בדרך זו. מבלי לתת חישובים, אנו מיד מסתכלים על הפקטור 0.1. מעניין אותנו כמה אפסים יש בו. אנו רואים שיש לו אפס אחד. כעת בשבר 3.25 נעביר את הנקודה העשרונית שמאלה בספרה אחת. העברת הפסיק ספרה אחת שמאלה, אנו רואים שאין יותר ספרות לפני השלוש. במקרה זה, הוסף אפס אחד ושם פסיק. כתוצאה מכך, אנו מקבלים 0.325

3.25 x 0.1 = 0.325

בוא ננסה להכפיל את 3.25 ב-0.01. תסתכל מיד על המכפיל של 0.01. מעניין אותנו כמה אפסים יש בו. אנו רואים שיש לו שני אפסים. כעת בשבר 3.25 נעביר את הפסיק שמאלה בשתי ספרות, נקבל 0.0325

3.25 x 0.01 = 0.0325

בוא ננסה להכפיל את 3.25 ב-0.001. הסתכל מיד על המכפיל של 0.001. מעניין אותנו כמה אפסים יש בו. אנו רואים שיש לו שלושה אפסים. כעת בשבר 3.25 נעביר את הנקודה העשרונית שמאלה בשלוש ספרות, נקבל 0.00325

3.25 × 0.001 = 0.00325

אל תבלבלו בין הכפלת עשרוניות ב-0.1, 0.001 ו-0.001 עם הכפלה ב-10, 100, 1000. טעות נפוצהרוב האנשים.

כאשר מכפילים ב-10, 100, 1000, הפסיק מזיז ימינה במספר ספרות כמו שיש אפסים במכפיל.

וכאשר מכפילים ב-0.1, 0.01 ו-0.001, הפסיק מועבר שמאלה במספר ספרות כמו שיש אפסים במכפיל.

אם בהתחלה קשה לזכור, אפשר להשתמש בשיטה הראשונה, שבה מבצעים את הכפל כמו במספרים רגילים. בתשובה, תצטרך להפריד את החלק השלם מהחלק השבר על ידי ספירת מספר הספרות בצד ימין כפי שיש ספרות אחרי הנקודה העשרונית בשני השברים.

מחלקים מספר קטן יותר במספר גדול יותר. שלב מתקדם.

באחד השיעורים הקודמים אמרנו שכאשר מחלקים מספר קטן במספר גדול יותר מתקבל שבר שבמונה שלו הדיבידנד ובמכנה המחלק.

לדוגמה, כדי לחלק תפוח אחד לשניים, צריך לכתוב 1 (תפוח אחד) במונה, ולכתוב 2 (שני חברים) במכנה. התוצאה היא שבריר. אז כל חבר יקבל תפוח. במילים אחרות, חצי תפוח. שבר הוא התשובה לבעיה איך לפצל תפוח אחד לשניים

מסתבר שאפשר לפתור את הבעיה הזו הלאה אם ​​מחלקים 1 ב-2. הרי פס שבר בכל שבר פירושו חלוקה, כלומר החלוקה הזו מותרת גם בשבר. אבל איך? אנחנו רגילים לכך שהדיבידנד תמיד גדול מהמחלק. וכאן, להיפך, הדיבידנד קטן מהמחלק.

הכל יתבהר אם נזכור ששבר פירושו ריסוק, חלוקה, חלוקה. המשמעות היא שניתן לפצל את היחידה לכמה חלקים שתרצו, ולא רק לשני חלקים.

כאשר מחלקים מספר קטן במספר גדול יותר, מתקבל שבר עשרוני, שבו החלק השלם יהיה 0 (אפס). החלק השברי יכול להיות כל דבר.

אז בואו נחלק 1 ב-2. בואו נפתור את הדוגמה הזו עם פינה:

אי אפשר לחלק אחד לשניים סתם ככה. אם תשאל שאלה "כמה שניים יש באחד" , אז התשובה תהיה 0. לכן, בפרטי נכתוב 0 ונשים פסיק:

כעת, כרגיל, נכפיל את המנה במחלק כדי לשלוף את השאר:

הגיע הרגע שבו ניתן לפצל את היחידה לשני חלקים. כדי לעשות זאת, הוסף עוד אפס מימין לאפס שהתקבל:

קיבלנו 10. נחלק 10 ב-2, נקבל 5. נכתוב את החמישה בחלק השבר של התשובה שלנו:

כעת אנו מוציאים את השארית האחרונה כדי להשלים את החישוב. תכפילו 5 ב-2, נקבל 10

קיבלנו את התשובה 0.5. אז השבר הוא 0.5

ניתן לכתוב חצי תפוח גם באמצעות השבר העשרוני 0.5. אם נוסיף את שני החצאים האלה (0.5 ו-0.5), נקבל שוב את התפוח המקורי השלם:

ניתן להבין נקודה זו גם אם נדמיין כיצד 1 ס"מ מתחלק לשני חלקים. אם מחלקים 1 ס"מ ל-2 חלקים, מקבלים 0.5 ס"מ

דוגמה 2מצא את הערך של ביטוי 4:5

כמה חמישיות יש בארבע? בכלל לא. אנחנו כותבים ב-0 פרטי ומכניסים פסיק:

נכפיל 0 ב-5, נקבל 0. נכתוב אפס מתחת לארבעה. הפחיתו מיד את האפס הזה מהדיבידנד:

כעת נתחיל לפצל (לחלק) את הארבעה ל-5 חלקים. לשם כך, מימין ל-4, נוסיף אפס ונחלק 40 ב-5, נקבל 8. נכתוב את השמונה באופן פרטי.

אנו משלימים את הדוגמה על ידי הכפלה של 8 ב-5, ומקבלים 40:

קיבלנו את התשובה 0.8. אז הערך של הביטוי 4: 5 הוא 0.8

דוגמה 3מצא את הערך של ביטוי 5: 125

כמה מספרים 125 יש בחמישה? בכלל לא. אנחנו כותבים 0 בפרטי ומכניסים פסיק:

נכפיל 0 ב-5, נקבל 0. נכתוב 0 מתחת לחמש. יש להחסיר מיד מהחמש 0

עכשיו בואו נתחיל לפצל (לחלק) את החמישה ל-125 חלקים. לשם כך, מימין לחמישה, אנו כותבים אפס:

חלקו 50 ב-125. כמה מספרים 125 יש ב-50? בכלל לא. אז במנה אנחנו שוב כותבים 0

נכפיל את 0 ב-125, נקבל 0. אנו כותבים את האפס הזה מתחת ל-50. מחסירים מיד 0 מ-50

כעת אנו מחלקים את המספר 50 ל-125 חלקים. לשם כך, מימין ל-50, נכתוב אפס נוסף:

חלקו 500 ב-125. כמה מספרים הם 125 במספר 500. במספר 500 יש ארבעה מספרים 125. אנחנו כותבים את הארבעה באופן פרטי:

אנו משלימים את הדוגמה על ידי הכפלה של 4 ב-125, ומקבלים 500

קיבלנו את התשובה 0.04. אז הערך של הביטוי 5: 125 הוא 0.04

חלוקה של מספרים ללא שארית

אז, בואו נשים פסיק במנה אחרי היחידה, ובכך מציין שהחלוקה של חלקים שלמים הסתיימה ונמשיך לחלק השבר:

הוסף אפס לשאר 4

כעת נחלק 40 ב-5, נקבל 8. אנו כותבים את השמונה באופן פרטי:

40–40=0. קיבל 0 בשאר. אז החלוקה הושלמה לחלוטין. חלוקה של 9 ב-5 מביאה לתוצאה עשרונית של 1.8:

9: 5 = 1,8

דוגמה 2. חלקו 84 ב-5 ללא שארית

ראשית נחלק 84 ב-5 כרגיל עם שארית:

התקבל בפרטי 16 ועוד 4 במאזן. כעת נחלק את השארית הזו ב-5. שמים פסיק בפרטי, ונוסיף 0 לשארית 4

כעת נחלק 40 ב-5, נקבל 8. נכתוב את השמונה במנה אחרי הנקודה העשרונית:

והשלם את הדוגמה על ידי בדיקה אם עדיין יש שארית:

חלוקת עשרוני במספר רגיל

שבר עשרוני, כידוע, מורכב ממספר שלם וחלק שברי. כאשר מחלקים שבר עשרוני במספר רגיל, קודם כל אתה צריך:

• חלקו את החלק השלם של השבר העשרוני במספר זה;
• לאחר חלוקת החלק השלם, עליך לשים מיד פסיק בחלק הפרטי ולהמשיך בחישוב, כמו בחלוקה רגילה.

לדוגמה, בואו נחלק את 4.8 ב-2

בוא נכתוב את הדוגמה הזו כפינה:

עכשיו בואו נחלק את כל החלק ב-2. ארבע חלקי שניים זה שניים. אנו כותבים את הצמד באופן פרטי ומיד שמים פסיק:

כעת נכפיל את המנה במחלק ונראה אם ​​יש שארית מהחילוק:

4-4=0. השאר הוא אפס. אנחנו עדיין לא כותבים אפס, מכיוון שהפתרון לא הושלם. אחר כך נמשיך לחשב, כמו בחלוקה רגילה. הורידו 8 וחלקו ב-2

8: 2 = 4. נכתוב את הארבעה במנה ומיד נכפיל אותה במחלק:

קיבלתי את התשובה 2.4. ערך ביטוי 4.8: 2 שווה 2.4

דוגמה 2מצא את הערך של הביטוי 8.43:3

נחלק 8 ב-3, נקבל 2. שים מיד פסיק אחרי השניים:

כעת נכפיל את המנה במחלק 2 × 3 = 6. נכתוב את השישה מתחת לשמונה ונמצא את היתרה:

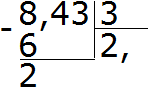
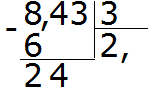
נחלק 24 ב-3, נקבל 8. נכתוב את השמונה באופן פרטי. מיד נכפיל אותו במחלק כדי למצוא את שאר החלוקה:

24–24=0. השאר הוא אפס. אפס עדיין לא נרשם. קח את שלושת הדיבידנדים האחרונים ונחלק ב-3, נקבל 1. נכפיל מיד 1 ב-3 כדי להשלים את הדוגמה הזו:

קיבלתי את התשובה 2.81. אז הערך של הביטוי 8.43: 3 שווה ל-2.81

חלוקת עשרוני בעשרוני

כדי לחלק שבר עשרוני לשבר עשרוני, בדיווידנד ובמחלק, הזיזו את הפסיק ימינה באותו מספר ספרות כמו שיש אחרי הנקודה העשרונית במחלק, ולאחר מכן מחלקים במספר רגיל.

לדוגמה, חלקו 5.95 ב-1.7

בואו נכתוב את הביטוי הזה כפינה

כעת, בדיווידנד ובמחלק, אנו מזיזים את הפסיק ימינה באותו מספר ספרות כמו שיש אחרי הנקודה העשרונית במחלק. למחלק יש ספרה אחת אחרי הנקודה העשרונית. אז עלינו להזיז את הפסיק ימינה בספרה אחת בדיווידנד ובמחלק. מעביר:

לאחר הזזת הנקודה העשרונית ימינה בספרה אחת, השבר העשרוני 5.95 הפך לשבר 59.5. והשבר העשרוני 1.7, לאחר הזזת הנקודה העשרונית ימינה בספרה אחת, הפך למספר הרגיל 17. וכבר יודעים לחלק את השבר העשרוני במספר הרגיל. חישוב נוסף לא קשה:

הפסיק מועבר ימינה כדי להקל על החלוקה. הדבר מותר בשל העובדה שכאשר מכפילים או מחלקים את הדיבידנד והמחלק באותו מספר, המנה אינה משתנה. מה זה אומר?

זה אחד מ תכונות מעניינותחֲלוּקָה. זה נקרא רכוש פרטי. חשבו על ביטוי 9: 3 = 3. אם בביטוי זה הדיבידנד והמחלק מוכפלים או מחולקים באותו מספר, אזי המנה 3 לא תשתנה.

בוא נכפיל את הדיבידנד והמחלק ב-2 ונראה מה קורה:

(9 × 2) : (3 × 2) = 18: 6 = 3

כפי שניתן לראות מהדוגמה, המנה לא השתנתה.

אותו דבר קורה כאשר אנו נושאים פסיק בדיבידנד ובמחלק. בדוגמה הקודמת, שבה חילקנו 5.91 ב-1.7, הזזנו את הפסיק ספרה אחת ימינה בדיווידנד ובמחלק. לאחר הזזת הפסיק, השבר 5.91 הומר לשבר 59.1 והשבר 1.7 הומר למספר הרגיל 17.

למעשה, בתוך התהליך הזה התרחש הכפל ב-10. כך זה נראה:

5.91 × 10 = 59.1

לכן, מספר הספרות אחרי הנקודה העשרונית במחלק תלוי במה יוכפל הדיבידנד והמחלק. במילים אחרות, מספר הספרות אחרי הנקודה העשרונית במחלק יקבע כמה ספרות בדיבידנד ובמחלק יוזז הפסיק ימינה.

חלוקה עשרונית ב-10, 100, 1000

חלוקת עשרוני ב-10, 100 או 1000 מתבצעת באותו אופן כמו . לדוגמה, בואו נחלק את 2.1 ב-10. בואו נפתור את הדוגמה הזו עם פינה:

אבל יש גם דרך שנייה. זה קל יותר. המהות של שיטה זו היא שהפסיק בדיבידנד מועבר שמאלה במספר ספרות כמו שיש אפסים במחלק.

בואו נפתור את הדוגמה הקודמת בדרך זו. 2.1: 10. אנו מסתכלים על המחלק. מעניין אותנו כמה אפסים יש בו. אנחנו רואים שיש אפס אחד. אז ב-2.1 המתחלק, אתה צריך להזיז את הפסיק שמאלה בספרה אחת. אנחנו מזיזים את הפסיק שמאלה בספרה אחת ורואים שלא נשארו יותר ספרות. במקרה זה, נוסיף עוד אפס אחד לפני המספר. כתוצאה מכך, אנו מקבלים 0.21

ננסה לחלק את 2.1 ב-100. יש שני אפסים במספר 100. אז ב-2.1 המתחלק, אתה צריך להזיז את הפסיק שמאלה בשתי ספרות:

2,1: 100 = 0,021

ננסה לחלק את 2.1 ב-1000. יש שלושה אפסים במספר 1000. אז ב-2.1 המתחלק, אתה צריך להזיז את הפסיק שמאלה בשלוש ספרות:

2,1: 1000 = 0,0021

חלוקה עשרונית ב-0.1, 0.01 ו-0.001

חלוקת עשרוני ב-0.1, 0.01 ו-0.001 מתבצעת באותו אופן כמו . בדיווידנד ובמחלק, אתה צריך להזיז את הפסיק ימינה במספר ספרות שיש אחרי הנקודה העשרונית במחלק.

לדוגמה, בואו נחלק את 6.3 ב-0.1. קודם כל, נעביר את הפסקים בדיווידנד ובמחלק ימינה באותו מספר ספרות כמו שיש אחרי הנקודה העשרונית במחלק. למחלק יש ספרה אחת אחרי הנקודה העשרונית. אז אנחנו מזיזים את הפסקים בדיווידנד ובמחלק ימינה בספרה אחת.

לאחר הזזת הנקודה העשרונית ימינה בספרה אחת, השבר העשרוני 6.3 הופך למספר הרגיל 63, והשבר העשרוני 0.1, לאחר הזזת הנקודה העשרונית ימינה בספרה אחת, הופך לאחד. ולחלק 63 ב-1 זה מאוד פשוט:

אז הערך של הביטוי 6.3: 0.1 שווה ל-63

אבל יש גם דרך שנייה. זה קל יותר. המהות של שיטה זו היא שהפסיק בדיבידנד מועבר ימינה במספר ספרות כמו שיש אפסים במחלק.

בואו נפתור את הדוגמה הקודמת בדרך זו. 6.3:0.1. בואו נסתכל על המפריד. מעניין אותנו כמה אפסים יש בו. אנחנו רואים שיש אפס אחד. אז ב-6.3 המתחלק, אתה צריך להזיז את הפסיק ימינה בספרה אחת. נעביר את הפסיק ימינה בספרה אחת ונקבל 63

בוא ננסה לחלק את 6.3 ב-0.01. למחלק 0.01 יש שני אפסים. אז ב-6.3 המתחלק, אתה צריך להזיז את הפסיק ימינה בשתי ספרות. אבל בדיבידנד יש רק ספרה אחת אחרי הנקודה העשרונית. במקרה זה, יש להוסיף עוד אפס אחד בסוף. כתוצאה מכך, אנו מקבלים 630

בוא ננסה לחלק את 6.3 ב-0.001. למחלק של 0.001 יש שלושה אפסים. אז ב-6.3 המתחלק, אתה צריך להזיז את הפסיק ימינה בשלוש ספרות:

6,3: 0,001 = 6300

משימות לפתרון עצמאי

אהבתם את השיעור?
הצטרף לקבוצת Vkontakte החדשה שלנו והתחל לקבל הודעות על שיעורים חדשים

פעולות עם שברים. במאמר זה ננתח דוגמאות, הכל מפורט עם הסברים. נשקול שברים רגילים. בעתיד, ננתח עשרוניות. אני ממליץ לצפות במלואו וללמוד ברצף.

1. סכום השברים, הפרש השברים.

כלל: כשמוסיפים שברים עם מכנים שווים, התוצאה היא שבר - המכנה שלו נשאר זהה, והמונה שלו יהיה שווה לסכוםמספרי שברים.

כלל: כשמחשבים את ההפרש של שברים עם אותם מכנים נקבל שבר - המכנה נשאר זהה, והמונה של השני מופחת מהמונה של השבר הראשון.

סימון פורמלי של הסכום וההפרש של שברים עם מכנים שווים:

דוגמאות (1):

ברור שכאשר נותנים שברים רגילים, אז הכל פשוט, אבל אם הם מעורבים? שום דבר מסובך...

אופציה 1- אתה יכול להמיר אותם לאלה רגילים ואז לחשב אותם.

אפשרות 2- אתה יכול בנפרד "לעבוד" עם החלקים השלמים והשברים.

דוגמאות (2):

יותר:

ואם ניתן הפרש של שני שברים מעורבים והמונה של השבר הראשון קטן מהמונה של השני? ניתן לעשות זאת גם בשתי דרכים.

דוגמאות (3):

* תורגם לשברים רגילים, חישב את ההפרש, המיר את השבר הלא תקין שהתקבל לשבר מעורב.

* מחלקים לחלקים שלמים ושברים, קיבלו שלושה, ואז הציג 3 כסכום של 2 ו-1, כשהיחידה מוצגת כ-11/11, ואז מצא את ההפרש בין 11/11 ל-7/11 וחישב את התוצאה. המשמעות של התמורות לעיל היא לקחת (לבחור) את היחידה ולהציג אותה כשבר עם המכנה שאנחנו צריכים, ואז מהשבר הזה אנחנו כבר יכולים להחסיר אחר.

דוגמה אחרת:

מסקנה: יש גישה אוניברסלית - על מנת לחשב את הסכום (ההבדל) של שברים מעורבים בעלי מכנים שווים, תמיד ניתן להמיר אותם לשברים לא תקינים, ואז לבצע את הפעולה הדרושה. לאחר מכן, אם כתוצאה מכך נקבל שבר לא תקין, אנו מתרגמים אותו לשבר מעורב.

לעיל, הסתכלנו על דוגמאות עם שברים בעלי מכנים שווים. מה אם המכנים שונים? במקרה זה, השברים מצטמצמים לאותו מכנה והפעולה שצוינה מתבצעת. כדי לשנות (להמיר) שבר, משתמשים בתכונה העיקרית של השבר.

שקול דוגמאות פשוטות:

בדוגמאות אלו, אנו רואים מיד כיצד ניתן להמיר את אחד השברים לקבלת מכנים שווים.

אם אנו מייעדים דרכים לצמצם שברים למכנה אחד, אז זה ייקרא שיטה ראשונה.

כלומר, מיד כאשר "מעריכים" את השבר, אתה צריך להבין אם גישה כזו תעבוד - אנו בודקים אם המכנה הגדול יותר מתחלק בקטן. ואם הוא מחולק, אז אנחנו מבצעים את ההמרה - נכפיל את המונה והמכנה כך שהמכנים של שני השברים יהיו שווים.

עכשיו תסתכל על הדוגמאות האלה:

להם גישה מוגדרתלא ישים. יש דרכים אחרות לצמצם שברים למכנה משותף, שקול אותם.

שיטה SECOND.

הכפל את המונה והמכנה של השבר הראשון במכנה של השני, ואת המונה והמכנה של השבר השני במכנה של הראשון:

*למעשה, אנו מביאים שברים לצורה כאשר המכנים הופכים שווים. לאחר מכן, אנו משתמשים בכלל של הוספת ביישן עם מכנים שווים.

דוגמא:

*שיטה זו יכולה להיקרא אוניברסלית, והיא תמיד עובדת. השלילי היחיד הוא שאחרי החישובים עשוי להתברר שבר שיהיה צורך לצמצם עוד יותר.

שקול דוגמה:

ניתן לראות שהמונה והמכנה מתחלקים ב-5:

שיטה שלישית.

מצא את הכפולה הפחות משותפת (LCM) של המכנים. זה יהיה המכנה המשותף. מה זה המספר הזה? זהו המספר הטבעי הקטן ביותר שמתחלק בכל אחד מהמספרים.

תראה, הנה שני מספרים: 3 ו-4, יש הרבה מספרים שמתחלקים בהם - אלה 12, 24, 36, ... הקטן שבהם הוא 12. או 6 ו-15, 30, 60, 90 הם מתחלק בהם.... לפחות 30. שאלה - איך לקבוע את הכפולה הפחות משותפת הזו?

יש אלגוריתם ברור, אבל לעתים קרובות זה יכול להיעשות מיד ללא חישובים. לדוגמה, לפי הדוגמאות לעיל (3 ו-4, 6 ו-15), אין צורך באלגוריתם, לקחנו מספרים גדולים (4 ו-15), הכפלנו אותם וראינו שהם מתחלקים במספר השני, אבל זוגות של מספרים יכולים להיות אחרים, כגון 51 ו-119.

אַלגוֹרִיתְם. על מנת לקבוע את הכפולה הפחות משותפת של מספר מספרים, עליך:

- לפרק כל אחד מהמספרים לגורמים פשוטים

- כתוב את הפירוק של BIGGER מהם

- הכפל אותו בגורמים החסרים של מספרים אחרים

שקול דוגמאות:

50 ו-60 50 = 2∙5∙5 60 = 2∙2∙3∙5

בפירוק יותרחסר אחד חמש

=> LCM(50,60) = 2∙2∙3∙5∙5 = 300

48 ו-72 48 = 2∙2∙2∙2∙3 72 = 2∙2∙2∙3∙3

בהרחבה של מספר גדול יותר חסרים שניים ושלושה

=> LCM(48,72) = 2∙2∙2∙2∙3∙3 = 144

* הכפולה הפחות משותפת של שני מספרים ראשוניים שווה למכפלתם

שְׁאֵלָה! ולמה זה שימושי למצוא את הכפולה הפחות משותפת, כי אתה יכול להשתמש בשיטה השנייה ופשוט להפחית את השבר המתקבל? כן, אתה יכול, אבל זה לא תמיד נוח. ראה מה יהיה המכנה של המספרים 48 ו-72 אם פשוט תכפיל אותם 48∙72 = 3456. תסכימי שיותר נעים לעבוד עם מספרים קטנים יותר.

שקול דוגמאות:

*51 = 3∙17 119 = 7∙17

בהרחבה של מספר גדול יותר, חסרה שלשה

=> LCM(51,119) = 3∙7∙17

ועכשיו אנו מיישמים את השיטה הראשונה:

* תסתכל על ההבדל בחישובים, במקרה הראשון יש מינימום מהם, ובשני צריך לעבוד בנפרד על פיסת נייר, ואפילו את השבר שקיבלת צריך להפחית. מציאת ה-LCM מפשטת את העבודה במידה ניכרת.

דוגמאות נוספות:

* בדוגמה השנייה ברור ש המספר הקטן ביותר, אשר מחולק ב-40 ו-60 שווה ל-120.

סה"כ! אלגוריתם חישוב כללי!

- אנו מביאים שברים לשברים רגילים, אם יש חלק שלם.

- אנו מביאים שברים למכנה משותף (תחילה נבדוק אם מכנה אחד מתחלק באחר, אם הוא מתחלק, אז נכפיל את המונה והמכנה של השבר האחר הזה; אם הוא אינו מתחלק, אנו פועלים דרך השני השיטות המצוינות לעיל).

- לאחר שקיבלנו שברים עם מכנים שווים, אנו מבצעים פעולות (חיבור, חיסור).

- במידת הצורך, אנו מצמצמים את התוצאה.

- במידת הצורך, בחר את כל החלק.

2. תוצר של שברים.

הכלל פשוט. כאשר מכפילים שברים, המונים והמכנים שלהם מוכפלים:

דוגמאות:

מְשִׁימָה. 13 טון ירקות הובאו לבסיס. תפוחי אדמה מהווים ¾ מכלל הירקות המיובאים. כמה קילוגרמים של תפוחי אדמה הובאו לבסיס?

בואו נסיים עם העבודה.

*קודם לכן הבטחתי לך לתת הסבר רשמי על המאפיין העיקרי של השבר דרך המוצר, בבקשה:

3. חלוקת שברים.

חלוקת השברים מצטמצמת לכפל שלהם. חשוב לזכור כאן שהשבר שהוא מחלק (זה שמחלקים בו) מתהפך והפעולה משתנה לכפל:

פעולה זו יכולה להיכתב כשבר של ארבע קומות, מכיוון שהחלוקה עצמה ":" יכולה להיכתב גם כשבר:

דוגמאות:

זה הכל! בהצלחה לך!

בברכה, אלכסנדר קרוטיסקיך.

שבריר- מספר המורכב ממספר שלם של שברים של אחד ומיוצג כ: a / b

מונה שברים (א)- המספר שמעל לקו השבר ומראה את מספר המניות שאליהן חולקה היחידה.

מכנה שבר (ב)- המספר מתחת לקו השבר ומראה כמה מניות חולקה היחידה.

2. הבאת שברים למכנה משותף

3. פעולות אריתמטיות על שברים רגילים

3.1. חיבור של שברים רגילים

3.2. חיסור של שברים רגילים

3.3. הכפלה של שברים רגילים

3.4. חלוקה של שברים רגילים

4. מספרים הדדיים

5. עשרוניות

6. פעולות אריתמטיות על שברים עשרוניים

6.1. הוספת עשרונים

6.2. חיסור של עשרונים

6.3. כפל עשרוני

6.4. חלוקה עשרונית

#1. תכונה בסיסית של שבר

אם המונה והמכנה של שבר מוכפלים או מחולקים באותו מספר שאינו שווה לאפס, אז יתקבל שבר השווה לנתון.

3/7=3*3/7*3=9/21 כלומר 3/7=9/21

a/b=a*m/b*m - כך נראית התכונה העיקרית של שבר.

במילים אחרות, אנו מקבלים שבר שווה לשבר הנתון על ידי הכפלה או חלוקה של המונה והמכנה של השבר המקורי באותו מספר טבעי.

אם ad=bc, ואז שני שברים a/b =c /d נחשבים שווים.

לדוגמה, השברים 3/5 ו-9/15 יהיו שווים, שכן 3*15=5*9, כלומר 45=45

הפחתת שברהוא תהליך של החלפת שבר, שבו השבר החדש שווה למקור, אך עם מונה ומכנה קטנים יותר.

נהוג לצמצם שברים על סמך התכונה העיקרית של שבר.

לדוגמה, 45/60=15/ ​ ​20 =9/12=3/4 ​ ​ ​ (המונה והמכנה מתחלקים ב-3, ב-5 וב-15).

שבר בלתי ניתן לצמצוםהוא חלק מהצורה 3/4 ​ ​ , כאשר המונה והמכנה הם הדדיים מספרים ראשוניים. המטרה העיקרית של הפחתת השבר היא להפוך את השבר לבלתי ניתן לצמצום.

2. הפחתת שברים למכנה משותף

כדי להביא שני שברים למכנה משותף:

1) הרחב את המכנה של כל שבר לתוך גורמים ראשוניים;

2) הכפל את המונה והמכנה של השבר הראשון בחסרים

גורמים מהרחבת המכנה השני;

3) הכפל את המונה והמכנה של השבר השני בגורמים החסרים מההרחבה הראשונה.

דוגמאות: צמצום שברים למכנה משותף.

בואו נפרק את המכנים לגורמים ראשוניים: 18=3∙3∙2, 15=3∙5

הכפלנו את המונה והמכנה של השבר בגורם החסר 5 מההרחבה השנייה.

מונה ומכנה של השבר לפי הגורמים החסרים 3 ו-2 מההרחבה הראשונה.

=, 90 הוא המכנה המשותף של שברים.

3. פעולות חשבון על שברים רגילים

3.1. חיבור של שברים רגילים

א) עם אותם מכנים, המונה של השבר הראשון מתווסף למונה של השבר השני, ומשאיר את המכנה זהה. כפי שניתן לראות בדוגמה:

a/b+c/b=(a+c)/b ​ ​ ;

ב) במכנים שונים מצטמצמים תחילה השברים למכנה משותף, ולאחר מכן מוסיפים את המונים לפי כלל א):

7/3+1/4=7*4/12+1*3/12=(28+3)/12=31/12

3.2. חיסור של שברים רגילים

א) עם אותם מכנים, הורידו את המונה של השבר השני מהמונה של השבר הראשון, ותותירו את המכנה זהה:

a/b-c/b=(a-c)/b ​ ​ ;

ב) אם המכנים של השברים שונים, אז תחילה מצמצמים את השברים למכנה משותף, ולאחר מכן חוזרים על השלבים כמו בפסקה א).

3.3. הכפלה של שברים רגילים

כפל שברים מציית לכלל הבא:

a/b*c/d=a*c/b*d,

כלומר, להכפיל את המונים והמכנים בנפרד.

לדוגמה:

3/5*4/8=3*4/5*8=12/40.

3.4. חלוקה של שברים רגילים

שברים מחולקים בצורה הבאה:

a/b:c/d=a*d/b*c,

כלומר, השבר a/b מוכפל בהדדיות של הנתון, כלומר, הוא מוכפל ב-d/c.

דוגמה: 7/2:1/8=7/2*8/1=56/2=28

4. מספרים הדדיים

אם a*b=1,אז המספר b הוא מספר הפוךלמספר א.

דוגמה: עבור המספר 9, ההפך הוא 1/9 ​ ​ , מאז 9*1/9 = 1 , עבור המספר 5 - מספר הדדי 1/5 ​ ​ , כי 5* ​ 1/5 ​ ​ = 1 .

5. עשרוניות

נקודהשקוראים לו חלק ראוי, שהמכנה שלו הוא 10, 1000, 10000, …, 10^n 1 0 , 1 0 0 0 , 1 0 0 0 0 , . . . , 1 0 ​ נ​ ​ .

לדוגמה: 6/10 =0,6; 44/1000=0,044 ​ .

באותו אופן, שגויים נכתבים עם מכנה 10^nאו מספרים מעורבים.

לדוגמה: 51/10= 5,1; 763/100=7,63

בצורה של שבר עשרוני, מיוצג כל שבר רגיל בעל מכנה שהוא מחלק בחזק מסוים של המספר 10.

מכנה, שהוא מחלק של חזקה מסוימת של המספר 10.

דוגמה: 5 הוא מחלק של 100, אז שבר 1/5=1 *20/5*20=20/100=0,2 ​ 0 = 0 , 2 .

6. פעולות חשבון על שברים עשרוניים

6.1. הוספת עשרונים

כדי להוסיף שני שברים עשרוניים, עליך לסדר אותם כך שאותן ספרות ופסיק מתחת לפסיק יופיעו זה מתחת לזה, ולאחר מכן להוסיף את השברים כמספרים רגילים.

6.2. חיסור של עשרונים

זה עובד באותו אופן כמו הוספה.

6.3. כפל עשרוני

כאשר מכפילים מספרים עשרוניים, מספיק להכפיל את המספרים הנתונים, תוך התעלמות מהפסיקים (כמספרים טבעיים), ובתשובה המתקבלת, הפסיק בצד ימין מפריד בין מספר הספרות שיש אחרי הנקודה העשרונית בשני הגורמים בסך הכל. .

בוא נעשה את הכפל של 2.7 ב-1.3. יש לנו 27\cdot 13=351 2 7 ⋅ 1 3 = 3 5 1 . אנו מפרידים שתי ספרות עם פסיק בצד ימין (למספר הראשון והשני יש ספרה אחת אחרי הנקודה העשרונית; 1+1=2 1 + 1 = 2 ). כתוצאה מכך, אנחנו מקבלים 2.7\cdot 1.3=3.51 2 , 7 ⋅ 1 , 3 = 3 , 5 1 .

אם התוצאה היא פחות ספרות ממה שצריך להפריד בפסיק, אז האפסים החסרים נכתבים מלפנים, למשל:

כדי להכפיל ב-10, 100, 1000, בשבר עשרוני, הזיזו את הפסיק 1, 2, 3 ימינה (במידת הצורך, מספר מסוים של אפסים מוקצים ימינה).

לדוגמה: 1.47 \cdot 10,000 = 14,700 1 , 4 7 ⋅ 1 0 0 0 0 = 1 4 7 0 0 .

6.4. חלוקה עשרונית

חלוקת שבר עשרוני במספר טבעי מתבצעת באותו אופן כמו חלוקת מספר טבעי במספר טבעי. פסיק בפרט מוצב לאחר השלמת חלוקת החלק השלם.

אם החלק השלם של הדיבידנד קטן מהמחלק, אז התשובה היא אפס מספרים שלמים, למשל:

שקול לחלק עשרוני בעשרוני. נניח שעלינו לחלק את 2.576 ב-1.12. קודם כל, נכפיל את הדיבידנד ואת המחלק של השבר ב-100, כלומר, נעביר את הפסיק ימינה בדיווידנד והמחלק במספר תווים שיש במחלק אחרי הנקודה העשרונית (בדוגמה זו , שתיים). אז אתה צריך לחלק את השבר 257.6 במספר הטבעי 112, כלומר, הבעיה מצטמצמת למקרה שכבר נחשב:

קורה שהשבר העשרוני הסופי לא תמיד מתקבל כאשר מחלקים מספר אחד במספר אחר. התוצאה היא אינסוף עשרוני. במקרים כאלה, עבור לשברים רגילים.

לדוגמה, 2.8: 0.09= 28/10: 9/100= 28*100/10*9=2800/90=280/9= ​ 31 1/9 ​ ​ .

כבר בפנים בית ספר יסודיתלמידים מתמודדים עם שברים. ואז הם מופיעים בכל נושא. אי אפשר לשכוח פעולות עם המספרים האלה. לכן, אתה צריך לדעת את כל המידע על שברים רגילים ועשרוניים. המושגים האלה פשוטים, העיקר להבין הכל לפי הסדר.

למה צריך שברים?

העולם סביבנו מורכב מחפצים שלמים. לכן אין צורך במניות. אבל חיי היום - יוםכל הזמן דוחף אנשים לעבוד עם חלקים של חפצים ודברים.

לדוגמה, שוקולד מורכב ממספר פרוסות. שקול את המצב שבו האריח שלו נוצר על ידי שנים עשר מלבנים. אם מחלקים אותו לשניים, מקבלים 6 חלקים. זה יהיה מחולק היטב לשלושה. אבל החמישה לא יוכלו לתת מספר שלם של פרוסות שוקולד.

אגב, הפרוסות האלה הן כבר שברים. וחלוקה נוספת שלהם מובילה להופעת מספרים מורכבים יותר.

מה זה "שבר"?

זהו מספר המורכב מחלקים של אחד. כלפי חוץ, זה נראה כמו שני מספרים מופרדים על ידי קו אופקי או לוכסן. תכונה זו נקראת שברים. המספר הכתוב למעלה (משמאל) נקרא מונה. זה בתחתית (מימין) הוא המכנה.

למעשה, פס השבר מתברר כסימן חלוקה. כלומר, ניתן לקרוא למונה דיבידנד, ולמכנה ניתן לכנות מחלק.

מהם השברים?

במתמטיקה יש רק שני סוגים מהם: שברים רגילים ושברים עשרוניים. תלמידי בית ספר מוצגים לראשונה בית ספר יסודי, קורא להם פשוט "שברים". השני לומד בכיתה ה'. אז מופיעים השמות האלה.

שברים נפוצים הם כל אלה שנכתבים כשני מספרים המופרדים בפס. לדוגמה, 4/7. עשרוני הוא מספר שבו לחלק השבר יש סימון מיקום והוא מופרד מהמספר השלם בפסיק. לדוגמה, 4.7. לתלמידים צריך להיות ברור ששתי הדוגמאות שניתנו הן מספרים שונים לחלוטין.

כֹּל שבר פשוטניתן לכתוב בתור עשרוני. הצהרה זו נכונה כמעט תמיד גם הפוך. ישנם כללים המאפשרים לכתוב שבר עשרוני כשבר רגיל.

איזה תת-מינים יש לסוגי השברים האלה?

עדיף להתחיל ב סדר כרונולוגיבזמן שהם נחקרים. השברים הנפוצים באים קודם. ביניהם ניתן להבחין ב-5 תת-מינים.

נכון. המונה שלו תמיד קטן מהמכנה.

לא בסדר. המונה שלו גדול או שווה למכנה.

ניתן לצמצום / בלתי ניתן לצמצום. זה יכול להיות נכון או לא נכון. דבר נוסף חשוב, האם למונה ולמכנה יש גורמים משותפים. אם יש, אז הם אמורים לחלק את שני חלקי השבר, כלומר להקטין אותו.

מעורב. מספר שלם מוקצה לחלק השבר הנכון (שגוי) הרגיל שלו. והוא תמיד עומד בצד שמאל.

מרוכבים. הוא נוצר משני שברים המחולקים זה לזה. כלומר, יש לו שלוש תכונות חלקיות בבת אחת.

לעשרונים יש רק שני תת-מינים:

סופי, כלומר כזה שבו החלק השבר מוגבל (יש לו סוף);

אינסופי - מספר שהספרות שלו אחרי הנקודה העשרונית אינן מסתיימות (ניתן לכתוב אותן בלי סוף).

איך להמיר עשרוני לרגיל?

אם זה מספר סופי, אזי מיושמת שיוך המבוסס על הכלל - כמו שאני שומע, אז אני כותב. כלומר, אתה צריך לקרוא אותו נכון ולכתוב אותו, אבל בלי פסיק, אבל עם קו שבר.

כרמז לגבי המכנה הנדרש, זכרו שזה תמיד אחד וכמה אפסים. את האחרון צריך לכתוב כמה כמו הספרות בחלק השבר של המספר הנדון.

איך להמיר שברים עשרוניים לשברים רגילים אם כל החלק שלהם חסר, כלומר שווה לאפס? לדוגמה, 0.9 או 0.05. לאחר החלת הכלל שצוין, מסתבר שאתה צריך לכתוב אפס מספרים שלמים. אבל זה לא מצוין. נותר לרשום רק את החלקים השברים. עבור המספר הראשון, המכנה יהיה 10, עבור השני - 100. כלומר, בדוגמאות המצוינות יהיו מספרים כתשובות: 9/10, 5/100. יתרה מכך, את האחרון מתברר שניתן להפחית ב-5. לכן, התוצאה עבורו חייבת להיכתב 1/20.

איך יוצרים שבר רגיל משבר עשרוני אם החלק השלם שלו שונה מאפס? לדוגמה, 5.23 או 13.00108. שתי הדוגמאות קוראות את החלק השלם וכותבות את ערכו. במקרה הראשון, זה 5, בשני, 13. אז אתה צריך לעבור לחלק השבר. איתם יש צורך לבצע את אותה פעולה. למספר הראשון יש 23/100, לשני יש 108/100000. יש להפחית שוב את הערך השני. התגובה היא כזו שברים מעורבים: 5 23/100 ו-13 27/25000.

איך ממירים אינסוף עשרוני לשבר מצוי?

אם זה לא תקופתי, אז לא ניתן לבצע פעולה כזו. עובדה זו נובעת מהעובדה שכל שבר עשרוני מומר תמיד לסופי או למחזורי.

הדבר היחיד שמותר לעשות עם שבר כזה הוא לעגל אותו. אבל אז המספר העשרוני יהיה שווה בערך לאין הסוף הזה. כבר אפשר להפוך אותו לרגיל. אבל התהליך ההפוך: המרה לעשרוני - לעולם לא ייתן ערך התחלתי. כלומר, אינסוף שברים לא מחזוריים אינם מתורגמים לשברים רגילים. יש לזכור זאת.

איך כותבים שבר מחזורי אינסופי בצורה של שבר רגיל?

במספרים אלו מופיעה תמיד ספרה אחת או יותר אחרי הנקודה העשרונית, שחוזרות על עצמן. הם נקראים מחזורים. לדוגמה, 0.3(3). כאן "3" בתקופה. הם מסווגים כרציונליים, מכיוון שניתן להמיר אותם לשברים רגילים.

מי שנתקל בשברים תקופתיים יודע שהם יכולים להיות טהורים או מעורבים. במקרה הראשון, הנקודה מתחילה מיד מהפסיק. בחלק השני, החלק השברי מתחיל במספרים כלשהם, ואז מתחילה החזרה.

הכלל שלפיו אתה צריך לכתוב אינסוף עשרוני בצורה של שבר רגיל יהיה שונה עבור שני סוגי המספרים הללו. די קל לכתוב שברים תקופתיים טהורים כשברים רגילים. כמו באחרונים, יש להמיר אותם: כתוב את הנקודה למונה, והמספר 9 יהיה המכנה, וחוזר על עצמו כמה פעמים שיש ספרות בתקופה.

לדוגמה, 0,(5). למספר אין חלק שלם, אז אתה צריך להמשיך מיד לחלק השברי. כתוב 5 במונה, ובמכנה כתוב 9. כלומר, התשובה תהיה השבר 5/9.

כלל כיצד לכתוב שבר עשרוני מצוי שהוא שבר מעורב.

תסתכל על אורך התקופה. כל כך הרבה 9 יהיה מכנה.

רשום את המכנה: קודם תשע, ואז אפסים.

כדי לקבוע את המונה, עליך לכתוב את ההפרש של שני מספרים. כל הספרות אחרי הנקודה העשרונית יקטן, יחד עם הנקודה. ניתן לחסר - זה ללא נקודה.

לדוגמה, 0.5(8) - כתוב את השבר העשרוני המחזורי כשבר מצוי. החלק השברי לפני התקופה הוא ספרה אחת. אז אפס יהיה אחד. יש גם רק ספרה אחת בתקופה - 8. כלומר יש רק תשע אחת. כלומר, צריך לכתוב 90 במכנה.

כדי לקבוע את המונה מ-58, צריך להחסיר 5. מסתבר ש-53. לדוגמה, תצטרך לכתוב 53/90 כתשובה.

כיצד מומרים שברים נפוצים לעשרונים?

האפשרות הפשוטה ביותר היא מספר שהמכנה שלו הוא המספר 10, 100 וכן הלאה. ואז המכנה פשוט מושלך, ומציבים פסיק בין החלק השבר והשלם.

ישנם מצבים שבהם המכנה הופך בקלות ל-10, 100 וכו'. לדוגמה, המספרים 5, 20, 25. מספיק להכפיל אותם ב-2, 5 ו-4, בהתאמה. רק יש צורך להכפיל לא רק את המכנה, אלא גם את המונה באותו מספר.

בכל שאר המקרים, כלל פשוט יועיל: חלקו את המונה במכנה. במקרה זה, אתה עשוי לקבל שתי תשובות: שבר עשרוני סופי או מחזורי.

פעולות עם שברים נפוצים

חיבור וחיסור

התלמידים מכירים אותם מוקדם יותר מאחרים. ובתחילה יש לשברים אותם מכנים, ואחר כך שונים. חוקים כללייםניתן לצמצם לתוכנית כזו.

מצא את הכפולה המשותפת הפחותה של המכנים.

כתוב גורמים נוספים לכל השברים הרגילים.

הכפל את המונים והמכנים בגורמים שהוגדרו עבורם.

הוסף (תחסיר) את המונים של השברים, והשאר את המכנה המשותף ללא שינוי.

אם המונה של המינואנד קטן מהמשנה, אז אנחנו צריכים לברר לפנינו מספר מעורבאו שבר ראוי.

במקרה הראשון, החלק השלם צריך לקחת אחד. הוסף מכנה למונה של שבר. ואז תעשה את החיסור.

בשני - יש צורך להחיל את כלל החיסור ממספר קטן יותר לגדול יותר. כלומר, הורידו את מודול ה-minuend מהמודלוס של ה-subtrahend, ושימו את הסימן "-" בתגובה.

הסתכלו היטב על תוצאת החיבור (חיסור). אם אתה מקבל שבר לא תקין, אז זה אמור לבחור את כל החלק. כלומר, מחלקים את המונה במכנה.

כפל וחילוק

לצורך יישומם, אין צורך לצמצם את השברים למכנה משותף. זה מקל על ביצוע הפעולה. אבל הם עדיין צריכים לציית לכללים.

כאשר מכפילים שברים רגילים, יש צורך לשקול את המספרים במונים ובמכנים. אם למונה ולמכנה כלשהו יש גורם משותף, ניתן לצמצם אותם.

תכפילו מספרים.

תכפילו את המכנים.

אם אתה מקבל שבר ניתן לצמצום, אז זה אמור להיות מפושט שוב.

כאשר מחלקים, תחילה עליך להחליף את החלוקה בכפל, ואת המחלק (שבר שני) בהדדיות (להחליף את המונה והמכנה).

לאחר מכן המשך כמו בכפל (החל משלב 1).

במשימות שבהן אתה צריך להכפיל (לחלק) במספר שלם, האחרון אמור להיכתב כשבר לא תקין. כלומר, עם מכנה של 1. לאחר מכן המשך כמתואר לעיל.



פעולות עם עשרוניות

חיבור וחיסור

כמובן, אתה תמיד יכול להפוך את השבר העשרוני לשבר משותף. ולפעול על פי התוכנית שתוארה כבר. אבל לפעמים יותר נוח לפעול בלי התרגום הזה. אז הכללים עבור החיבור והחיסור שלהם יהיו זהים לחלוטין.

השווה את מספר הספרות בחלק השבר של המספר, כלומר אחרי הנקודה העשרונית. הקצה את המספר החסר של אפסים בו.

כתוב שברים כך שהפסיק יהיה מתחת לפסיק.

הוסף (חיסור) כמו מספרים טבעיים.

הסר את הפסיק.

כפל וחילוק

חשוב שלא תצטרכו להוסיף כאן אפסים. שברים אמורים להישאר כפי שהם ניתנים בדוגמה. ואז ללכת לפי התוכנית.

בשביל הכפל, אתה צריך לכתוב שברים אחד מתחת לשני, בלי לשים לב לפסיקים.

הכפל כמו מספרים טבעיים.

שים פסיק בתשובה, סופר מהקצה הימני של התשובה כמה ספרות שיש בחלקים השברים של שני הגורמים.

לחלק צריך קודם להמיר את המחלק: לעשות אותו מספר טבעי. כלומר, הכפלו אותו ב-10, 100 וכו', תלוי בכמה ספרות יש בחלק השבר של המחלק.

הכפל את הדיבידנד באותו מספר.

מחלקים עשרוני במספר טבעי.

שים פסיק בתשובה ברגע שבו מסתיימת החלוקה של כל החלק.



מה אם יש שני סוגי השברים בדוגמה אחת?

כן, במתמטיקה יש לעתים קרובות דוגמאות שבהן אתה צריך לבצע פעולות על שברים רגילים ועשרוניים. ישנם שני פתרונות אפשריים לבעיות אלו. אתה צריך לשקול באופן אובייקטיבי את המספרים ולבחור את הטוב ביותר.

דרך ראשונה: מייצגים עשרוניות רגילות

זה מתאים אם, בעת חלוקה או המרה, מתקבלים שברים סופיים. אם לפחות מספר אחד נותן חלק תקופתי, אז הטכניקה הזו אסורה. לכן, גם אם אתה לא אוהב לעבוד עם שברים רגילים, תצטרך לספור אותם.

הדרך השנייה: כתוב שברים עשרוניים כרגילים

טכניקה זו נוחה אם יש 1-2 ספרות בחלק שאחרי הנקודה העשרונית. אם יש יותר מהם, אתה יכול לקבל חלק גדול מאוד רגיל ו ערכים עשרונייםיאפשר לך לחשב את המשימה מהר יותר וקל יותר. לכן, תמיד יש צורך להעריך בצורה מפוכחת את המשימה ולבחור בשיטת הפתרון הפשוטה ביותר.