הפרוצדורה למעבר ממסננים אנלוגיים למסננים דיגיטליים נקראת שיטת ה-impulse response invariance.

אורז. 12.9. הליך חישוב על ידי שיטת אינוריאנטיות של תגובת דחפים. (ראה סריקה)

הליך זה קובע שתגובת הדחף של המסנן הדיגיטלי המתקבל היא דגימות תגובת הדחף של המסנן האנלוגי המתאים והיא מוגדרת כדלקמן:

כאשר T הוא מרווח הדגימה. הליך התכנון לשיטה זו מוצג באיור. 12.9.

כדי להמחיש את שיטת אי-התגובת הדחף

אנו מרחיבים את פונקציית ההעברה של המסנן האנלוגי המקורי לתוך שברים פשוטים

כאשר אנו מניחים זאת וכל הקטבים שונים. בנוסף, עבור כל אחד מהם הוא הקוטב של המסנן האנלוגי, והוא שייר הפונקציה בקוטב. ניתן לקבל את תגובת הדחף של המסנן האנלוגי ע"י ביצוע טרנספורמציה לפלס הפוכה של המשוואה (12.29), הנותנת

היכן רצף הצעדים של היחידה. החלפת ביטוי (12.30) בנוסחה (12.28), נקבל את תגובת הדחף של המסנן הדיגיטלי המתאים

היכן רצף הצעדים של היחידה. פונקציית ההעברה של המסנן הדיגיטלי המתקבל נקבעת על ידי מציאת ה-transform של תגובת הדחף הניתנת על ידי ביטוי (12.31) באופן הבא:

בהשוואה בין ביטויים (12.29) ו-(12.32), אנו מקבלים את יחס המעבר ממסננים אנלוגיים למסננים דיגיטליים עבור שיטת איווריאנטיות תגובת הדחפים, בעלת הצורה

עמוד סינון דיגיטלי המתאים לעמוד סינון אנלוגי

דוגמה 12.2. למסנן האנלוגי המקורי יש את פונקציית ההעברה הבאה:

פִּתָרוֹן. אנו כותבים את הפונקציה בצורה של שברים פשוטים

עולה ממשוואות (12.33) שיש לו את הצורה

כאשר T הוא מרווח הדגימה. בפשטת הביטוי (12.36 א), נקבל

דוגמה 12.3. מסנן מנורמל מסדר שני Chebyshev נמוך עם אדוות פס פס של 3 dB יש פונקציית העברה של הטופס

מצא את פונקציית ההעברה של המסנן הדיגיטלי המתאים באמצעות שיטת אי-התגובת הדחף.

פִּתָרוֹן. כתיבת הפונקציה בצורה של גורמים, אנו מקבלים

החלת משוואות (12.33) על היחס המתקבל נותן

עבור c, משוואה (12.39) מרמזת על כך

אורז. 12.10. מאפייני משרעת-תדר של מסנן Chebyshev מהסדר השני עם אי אחידות של 3 dB. פילטר אנלוגי, - פילטר דיגיטלי, מסנן דיגיטלי

מאפייני המשרעת-תדר של הפונקציות הניתנות על ידי ביטויים (12 40) ו- (12.41) מוצגים באיור. 12 10

נזכיר כי הפונקציה המחזורית של המשתנה 0 עם נקודה אינה מחזורית.ההבדל העיקרי במאפיינים של מסננים אנלוגיים ודיגיטליים הוא שמאפייני המשרעת-תדר של המסנן הדיגיטלי המתקבל יחרגו מהמאפיינים של המסנן האנלוגי המקורי. באותם קטעים שבהם העקומה האופיינית מגיעה לנקודות או - דיסקרטיזציה של מרווחים. אם מרווח הדגימה קטן מספיק, הסטייה תתחיל בנקודה הקרובה ל. אחרת, הסטייה תתחיל הרבה יותר מוקדם. מקרה מתאים מוצג באיור. 12.10. יש לציין כי תדרי החיתוך של מסננים דיגיטליים ממוקמים בנקודות

שבו נעשה שימוש במידע על תדר החיתוך של המסנן האנלוגי. תדרי החיתוך הללו חוזרים על עצמם בהתאם לקשר הבא:

מאחר שתגובת האימפולסים של מסנן דיגיטלי הנגזרת משיטת אינוריאנטיות תגובת האימפולס היא למעשה האנלוגי הנדגם של תגובת האימפולסים של מסנן אנלוגי, תגובת התדר של מסנן דיגיטלי היא גרסה מרוכזת של תגובת תדר המסנן האנלוגי כפי שנקבעה במשוואה (11.115) והוא מצוטט שוב ​​כאן מטעמי נוחות. :

אם קצב הדגימה מהיר מספיק, אז אפקט הכינוי הוא מינימלי. על איור. 12.10 עבור c מראה שקשה להבחין באפקט הכינוי, המתבטא בצורה של סטייה בתגובות התדר של מסננים אנלוגיים ודיגיטליים. עם זאת, עם לא מספיק מהירות גבוההדיסקרטיזציה, למשל, עבור המקרה (איור 12.10), אפקט הסופרפוזיציה מתחיל להשפיע, מכיוון שניתן לראות שהוא שונה במידה ניכרת מהחלפה למשוואות (12.43), אנו מקבלים

יש לציין שמשוואות (12.44) קובעות את הקשר בין פונקציות ההעברה של המסנן הדיגיטלי והמסנן האנלוגי המתאים למקרה של אי-ווריאציה של תגובות הדחף שלהם.

ללמוד את המאפיינים עם השיטה של ​​אינווריאציה של תגובת הדחף לעמידה בשני הכרחי

תנאי הליך המעבר (12.10), שקול את הקשר

ולכן

מתוך איור. 12.11 יוצא שרצועה אופקית עם רוחב במישור s מוצגת בכל המישור, כלומר, החצאים השמאלי והימני של רצועה זו מוצגים בהתאמה בחלק של המישור בתוך ומחוץ למעגל היחידה, והציר הדמיוני - במעגל היחידה. מתוך איור. 12.11 ניתן לקבוע כי מקור אפקט השכבה נגרם מכך שהמעבר (12.45) אינו ייחודי. לדוגמה, נקודות ממפות לנקודה בודדת.למעשה, יחסים (12.45) קובעים שפונקציית ההעברה האנלוגית בכל פס רוחב מונחת על כל המישור כדי ליצור פונקציית העברה דיגיטלית. לפיכך, שיטת איווריאנטיות תגובת הדחפים אינה מיפוי ליניארי פשוט או דומה ממישור ה-s למישור -מישור. בשל אפקט הכינוי, שיטת ה-impulse response invariation ישימה רק על מסננים עם תגובת תדר אנלוגי מוגבלת משמעותית העומדת בתנאי

כלומר, במקרים של מסנני מעבר נמוך ופס פס.

כפי שמוצג, הליך המעבר המבוסס על שיטת אינוריאנטיות תגובת דחפים ניתן על ידי משוואות (12.33), הקובעות שמיקום הקוטב של המסנן האנלוגי ממופה למיקום הבא:

לפיכך, יחסים (12.45) מבססים קשר בין מיקומי הקוטב של המסננים האנלוגיים והדיגיטליים. עם זאת, הקביעה כי היחסים

(לחץ לצפייה בסריקה)

אורז. 12.12. דיאגרמות של הקטבים והאפסים של מסנן לרנר מהסדר השני: a - וריאנט של המסנן האנלוגי, b - וריאנט של המסנן הדיגיטלי המתקבל על בסיס שיטת איווריאנטיות תגובת הדחפים.

(12.45) קובעים את הקשר בין מיקומי האפסים של המסננים הדיגיטליים והאנלוגיים עם השונות של תגובות הדחף. דוגמה מתאימה היא העוקב.

דוגמה 12.4. פונקציית ההעברה של המסנן האנלוגי מוגדרת

שבו מצא את מיקומם של האפסים והקטבים של המסנן הדיגיטלי המתקבל על בסיס האינווריאנטיות של תגובת הדחף. פִּתָרוֹן. פירוק הפונקציה לשברים פשוטים נותן

פונקציית ההעברה של המסנן הדיגיטלי המתאים ניתנת לפי (12.33) as

מתוך משוואה (12.50), המיקום של האפס הקצה של המסנן הדיגיטלי ניתן על ידי

איפה המיקום של האפס של המסנן האנלוגי. עם זאת, הקטבים של המסנן הדיגיטלי מסודרים באופן הבא:

איפה המיקום של הקטבים של המסנן האנלוגי. התרשים של מיקום הקטבים והאפסים של המסננים האנלוגיים והדיגיטליים המתאימים מוצג באיור. 12.12.

נמצא כי משוואות (12.33) חלות הן על קטבים אמיתיים והן על קטבים מורכבים. עם זאת, עבור קוטב מורכב נוח יותר לשקול זוג קטבים יחדיו כאשר פס מעל משתנה משמש לציון הצמוד המורכב. יישום משוואות (12.33) בהתאם, נקבל זוגות של טרנספורמציות עבור שני המקרים הבאים מהסדר השני:

1. אם פונקציית ההעברה של המסנן האנלוגי ניתנת כ

היכן ממוקמים הקטבים בנקודות

אז לפונקציית ההעברה של המסנן הדיגיטלי המתאים יש את הצורה

2. אם הפונקציה ניתנת בטופס

אז נובע מהליך המעבר (12.33) כי

דוגמה 12.5. למסנן המעבר הנמוך האנלוגי מסדר שלישי של Butterworth יש את פונקציית ההעברה הבאה:

מצא את פונקציית ההעברה של מסנן Butterworth הדיגיטלי התואם מסדר שלישי באמצעות שיטת אי-השוואת תגובת הדחפים,

פִּתָרוֹן. ניתן לכתוב את הפונקציה בתור

ממשוואות (12.33), (12.53)-(12.56) למסנן הדיגיטלי הנדרש יש את פונקציית ההעברה הבאה:

דוגמה 12.6. נניח שהספרות של מסנן המעבר הנמוך שלך חייבות לעמוד בתנאים הבאים:

א) תדר החיתוך של 3 dB הוא rad.

ב) חוסר האחידות של מאפיין המשרעת-תדר בפס המעבר אינו עולה על 0.1 dB עבור rad.

ג) הנחתת פס עצור גדולה מ-30 dB עבור רד.

ד) למאפיין משרעת-תדר יש צורה מונוטונית יורדת עבור

ה) מרווח דגימה

מצא את פונקציית ההעברה של המסנן הדיגיטלי הרצוי.

פִּתָרוֹן. בשלב הראשון, יש צורך להמיר קריטריונים דיגיטליים אלה לאנלוגיים. ניתן לעשות זאת, בהתחשב בכך שאם T עומד בקריטריון Nyquist, משוואות (12-43) מצטמצמות בערך לצורה

ולכן

על פי יחס (12.606), המסנן האנלוגי הרצוי חייב לעמוד בדרישות הבאות:

א) תדר החיתוך של 3 dB הוא

אנו ממשיכים בהיכרות עם שיטות פתרון אנליטיות משימות מאתגרותעם הפרמטרים המוצעים בבדיקות שונות ובמציאות השתמש באפשרויות. בחומר של היום, נשקול קבוצה חדשה של משימות הקשורות לחיפוש אחר ערכי הפרמטר(ים) שעבורם יש הדבר היחידהפתרון של הבעיה. מִלָה « הדבר היחיד » בנושא זה הוא המפתח. אחת השיטות הנפוצות ביותר לפתרון בעיות כאלה היא מה שנקרא שיטת שורש סימטריתאו, יותר מדעית, שיטת אינווריאציה.

ניסוחים אופייניים של משימות כאלה הם כדלקמן: א, שעבורו יש למערכת המשוואות החלטה בלבד.» אוֹ: "מצא את כל ערכי הפרמטרים אעבור המשוואה יש שורש בודד.

אז, הגיע הזמן להכיר את האינבוריות. מה זה הקונספט הזה? תורגם לרוסית, המילה "אינווריות"אומר "בלתי משתנה". חוסר השינוי של משהו ביחס למשהו.)

במתמטיקה, אינווראנס מובנת כ חוסר השינוי של כל ביטוי עם משתנים או פונקציות ביחס לכל טרנספורמציותעל אותם משתנים. זה יכול להיות החלפה של משתנה אחד באחר, שינוי סימן וכו'. במילים, זה אולי לא נשמע ממש ברור, אבל במציאות הכל הרבה יותר פשוט.

הבה נבחן דוגמה פשוטה. כולנו עם בית ספר יסודיאנו מכירים (אני מאמין!) את התכונה הקומוטטיבית של הוספת שני מספרים:

a + b = b + a.

מי יתווכח, נכון? הסכום אינו משתנה מהסידור מחדש של המונחים.) מבחינה מדעית, עובדה זו פירושה שהביטוי a + b בלתי משתנהעל החלפת a ב-b ו-b ב-a. אתה יכול להחליף אותיות כמה שאתה רוצה, אבל המהות של הביטוי כולו לא תשתנה מהתמורות שלנו.)

דוגמה קלאסית נוספת לאינוריאנטיות היא שִׁוּוּי. אם הפונקציה f(x) זוגית, אז, כידוע,

F(-x) = f(x),

ואז נוכל לומר שהפונקציה f(x) בלתי משתנה יחסית תחליפים איקס עַל – איקס .

בואו נסתכל על השונות בחיים?

נניח שיש לנו את המשוואה המגניבה הזו:

x + y = 10

כפי שאתה יכול לראות, יש לו אינסוף פתרונות. אלו הם, למשל, זוגות של מספרים (1; 9), (5; 5), (0; 10), (-37; 47), וכן הלאה, אתה יכול לכתוב עד שאתה כחול בפנים. ) למה אתה שואל? לעת עתה - אין צורך. עבודה מטופשת, למען האמת. אבל מכיוון שכידוע הסכום אינו משתנה מסידור מחדש של מונחים, כל הפתרונות הללו מאוחדים על ידי תכונה חשובה אחת: אם זוג מספרים כלשהו (x 0 ; y 0) עונה על המשוואה הזו, ואז אוטומטית את צמד המספרים (y 0 ; x 0) גַםבהחלט מספק אותו . או במקרים כאלה אומרים שהמשוואה

x+y=10

בלתי משתנה יחסית החלפות xעַלy ו yעַלאיקס. לדוגמה, אם זוג (1;9) הוא פתרון, אז אוטומטית (9;1) הוא גם פתרון. הבנתי, אני חושב.)

מי שיודע לפתור מערכות ומודע לאופן חשיפת המודולים, הוא יקבל בקלות שמונה מהפתרונות שלה. אלו הזוגות:

(1; 2), (2; 1), (-1; 2), (2; -1), (1; -2), (-2; 1), (-1; -2); (-2; -1).

כמה יפה המערכת הזו? והעובדה שיש לו שלושה סוגים של אינווריאציה בבת אחת!

תראה בעצמך.

ראשית, מהות המערכת לא תשתנה מההחלפה איקסעַל yו yעַל איקס. זה אומר, בנוסף לזוג(x0; y 0), למערכת יש גם זוג (y 0 ; x 0) כפתרון שלה. לדוגמה, אלו הם זוגות (1; 2) ו-(2; 1) או (-1; -2) ו-(-2; -1). וכולי.

שנית, הריבוע והמודלוס הם אפילו פונקציות. המשמעות היא שמהות המערכת לא תשתנה מההחלפה, למשל, איקסעַל -איקס. לכן, בנוסף לזוג (x 0 ; y 0), הפתרון של המערכת יהיה גם הזוג (-x 0 ; y 0). מה שבא לידי ביטוי, למשל, בזוגות (1; 2) ו-(-1; 2). או (2; 1) ו-(-2; 1).

אותו הדבר ניתן לומר על המשתנה y: מהות המערכת אינה משתנה מההחלפה yעַל -י, שכן הריבוע והמודלוס שורפים מינוס. ובנוסף לזוג (x 0; y 0), הפתרון למערכת שלנו יהיה גם הזוג (x 0; -y 0). לדוגמה, זוגות (1; 2) ו-(1; -2).

האם הרעיון ברור?

עכשיו בואו נדמיין שיש לנו איזושהי מערכת מאוד מפחידה. ואיכשהו קבענו באורח פלא שהמערכת הזו היא בלתי משתנה תחת, למשל, החלפת x ב-y. במקרה זה, הבעיה דורשת שהפתרון יהיה היחיד. לאחר מכן בהכרחהשוויון חייב להתקיים איקס = y . כלומר, פתרון ייחודי כזה יכול להיות רק זוג מספרים (x 0 ; x 0) (או (y 0 ; y 0), שזהו במקרה זה).

ועכשיו בכל המשימה אנחנו יכולים בכל מקום באומץ החלף את y ב-x(או להיפך) וללכת אל אחדמשתנה, אשר, ככל הנראה, מפשט מאוד חישובים נוספים.)

או אם בבעיה כלשהי הארגומנט x נמצא בכל מקום בסימן של פונקציה זוגית - ריבוע, מודולוס, קוסינוס וכו', ונדרש שפתרון הבעיה יהיההיחיד, אז זה יהיה אפשרי רק אם

איקס = - איקס ,

זה,

איקס = 0 .

למה? כן, כי עבור כל שאר ה-x שאינם אפס, המספר –x יהיה אוטומטית גם פתרון, כלומר. המשימה בהחלט תהיהיותר מפתרון אחד. ועכשיו אתה יכול להחליף x=0לתוך הבעיה המקורית ולפשט אותה באופן משמעותי. לפיכך, במקרה של זוגיות, מה שנקראסימטריה סביב האפס.

אבל סימטריה היא לא רק ביחס לאפס. אם, נניח, המשוואה לא משתנה ביחס להחלפה איקסעַל 2- איקסוחייב להיות שורש יחיד, אם כן בהכרחהשוויון חייב להתקיים

x = 2 - x

אוֹ

x = 1.

כלומר, השורש היחיד הזה יכול להיות רק אחד. ועכשיו כבר אפשר להחליף את x = 1 במשוואה המקורית ולקבוע את כל הערכים של הפרמטר שעבורו היחידה היא השורש.

יש גם סטיות פחות ברורות. לדוגמה, לגבי החלפת x ב-1/x, שמכאן המספרים היחידים ±1 יכולים להיות מועמדים לפתרון ייחודי. וכולי. החיפוש אחר דפוסים כאלה הוא לפעמים תהליך יצירתי ומעניין מאוד, ובעיות מסוג זה מיועדות למתמודדים על ציונים גבוהים.)

תהליך פתרון בעיות כאלה מורכב מארבעה שלבים מרכזיים.

1) בדיקת הבעיה וזיהוי מבנים בלתי משתנה. למשל, ביטויים איקס ו -איקס, y ו y-1 וכולי.

2) מציאת פתרונות מועמדים לייחודיות. זה נעשה על ידי השוואת המבנים הבלתי משתנים ביותר זה לזה ופתרון המשוואה המתקבלת.

3) החלפת פתרונות מועמדים לבעיה המקורית וחיפוש ערכי פרמטרים התואמים לפתרונות אלו.

4) בדיקת כל ערך פרמטר שנמצא על סיפוק תנאי הבעיה.

השלב הרביעי הוא מאוד ( מאוד!) חשוב בפתרון בעיות כאלה! הסברים בהמשך. על דוגמאות.

אוקיי, סיפור ההקדמה הארוך הסתיים, עכשיו בואו נעבור ל משימות ספציפיות(כולל אלה מבחינת המדינה המאוחדת) ואנו נפתור אותם ככל שהמורכבות תגבר. נתחיל בקטן - עם משוואות. :)

דוגמה 1

אז, אנחנו מדברים על שורש בודד. זוהי קריאה ברורה לחפש מבנים בלתי משתנה במשוואה.)

רק הצד השמאלי תלוי ב-x. בוא נכתוב את זה בנפרד:

3 x + 3 2 x.

עכשיו בואו נדבר ככה:

"יש לנו סכום של שני ביטויים אקספוננציאליים בצד שמאל. הבסיסים שלהם זהים - שלושה. וזה טוב מאוד.) אבל האינדיקטורים שונים. "x" ו-"שניים מינוס x". אבל! אם בקדנציה הראשונה האינדיקטוראיקסהוחלף על ידי 2, ולהיפך בשני2הוחלף על ידי איקס, אז המונחים פשוט יחליפו מקומות, ומהות הביטוי כולו לא תשתנה.

ממש צודק! משוואה זו היא בלתי משתנה תחת השינוי איקסעַל 2! במילים אחרות, אם מספר כלשהו x 0הוא השורש של המשוואה הזו, ואז אוטומטית המספר 2-x 0גַםיהיה השורש שלו.)

במקרה שלנו, לפי תנאי, השורש חייב להיות ייחודי. לכן, זה אפשרי אם ורק אם

x 0 = 2 x 0

אוֹ

X 0 \u003d 1.

כאן מה שנקרא סימטריה על אחדות.

זה אומר שאם למשוואה הזו יש שורש בודד, אז זה יכול להיות רק אחד. ועכשיו אתה יכול להחליף x = 1לתוך המשוואה המקורית וקבע באילו ערכים של הפרמטר אזה יבוצע. אנו מחליפים:

אנחנו פותרים את זה משוואה ריבועית. הדרך הקלה ביותר היא לפי משפט וייטה:

קיבלנו שני ערכי פרמטרים - אחד וחמישה. אבל (תשומת הלב!)זה עדיין לא תשובה, אבל רק שניים אפשריים מוּעֲמָדלתשובה.) עכשיו אנחנו עדיין צריכים לעשות את השלב האחרון - לבדוק כל ערך פרמטר א למלא את התנאי של ייחוד השורש.

אני מתמקד במיוחד בשלב האחרון של הפתרון. בשום פנים ואופן אסור לפספס את זה. למה?

נראה שהכל מגניב: נמצאו הפרמטרים, וזה אמור להשלים את פתרון הבעיה ולרשום את התשובה. אבל... נאלץ לחשוף את האמת המרה. העניין הוא שערכי הפרמטרים שנמצאו בשלב השלישי הם רק מה שנקרא נחוץ תנאי לייחודיות הפתרון. אבל לרוע המזל, לא מספיק!אני מסביר.

שני המספרים שנמצאו (1 ו-5) הם הערכים של הפרמטר,נחוץכך שהיחידה בלבדהיה השורש של המשוואה הזו. וזה הכל! אם זה יהיה השורש היחיד או לא זה בכלל לא עובדה!

לכן, השלב האחרון (והחובה!) של הפתרון הוא בדיקת ספיקות. זה נעשה ככה. כל אחד מערכי הפרמטר שנמצאו נלקח ומוחלף לתוך התחלתימְשִׁימָה. לאחר מכן אנו פותרים את הבעיה המקורית עבור כל מועמד כזה וקובעים כמה פתרונות יתקבלו בכל מקרה. המועמדים שעבורם לבעיה יש יותר מפתרון אחד מנוקרים ללא רחמים.)

יש לומר שהשלב האחרון בבעיות כאלה הוא לרוב האורך ביותר, מכיוון שהוא לא תמיד מביא למשוואות ומערכות שניתן לפתור על ידי טרנספורמציות אלגבריות סטנדרטיות - פירוק לגורמים, הפחתה של דומות, נוסחאות טריגונומטריות, לוגריתמים, וכו ' ולפעמים דורשים כושר המצאה ואמנות ניכרים, הייתי אפילו אומר. כפי שנראה בעצמנו בדוגמאות הבאות.)

לכן, אנו לוקחים כעת את ערכי הפרמטרים המצויים שלנו ו להחליף לתוך המשוואה המקורית.

בוא נתחיל עם a = 1. אנחנו פשוט לוקחים ומחליפים לתוך המשוואה במקום " א"(ולא x!) אחד:

על פי כללי הפעולה עם תארים:

הבה נשכתב את המשוואה שלנו עם העובדה הזו בחשבון:

הכפל את שני הצדדים במכנה 3 x(זה די לא מזיק, מאז הביטוי3 xחיובי עבור כל x ולעולם אינו שווה לאפס) והזיז הכל שמאלה:

יש משוואה ריבועית עבור3 x.

אפילו לא צריך להחליף אותו.3 x = t, אבל די לציין שמשמאל נמצא ריבוע מלאהבדלים:

אומר,

אז, ב a = 1המשוואה המקורית בֶּאֱמֶתיש אחדות כשורש הייחודי שלה. אומר, a = 1אנחנו לגמרי מרוצים ומגיבים.

עכשיו בואו נתמודד עם החמישה a=5. ניקח ונחליף את החמש במשוואה המקורית במקום א:

קיבלנו משוואה שווה בדיוק למקרה a = 1, שכפי שכבר נקבע, יש לו יחידת שורש אחת. אז גם החמישה מתאימים לנו: a=5.

אז, הוכחנו באופן מלא ששני הערכים שנמצאו של הפרמטר עומדים בתנאי הספיקות, כלומר. למשוואה המקורית יש באמת שורש בודד, והשורש הזה הוא x = 1. וכך עַכשָׁיואתה יכול לרשום את התשובה הסופית במצפון טוב.)

תשובה: a=1; a=5.

אגב, ניתן לפתור את אותה בעיה, כמובן, באמצעות שינוי המשתנה הנ"ל3 x = t, עברו למשוואה ריבועית (כבר ביחס ל-t) עם פרמטר והעמידו תנאי לייחודיות השורש. איזה? כמובן, שוויון לאפס של המפלה.) אבל, שכן נושא השיעור הזה הוא חוסר שונות, ואז פתרנו את זה באמצעות האינווריאנס בדיוק.) ובכל זאת, טוב שיש כמה דרכים לפתור את אותה בעיה, מסכים.)

כאן, בדיקת הספיקות לא השפיעה בשום צורה על התשובה. בַּר מַזָל דוגמה טובה.) אבל, שוב, השלב הזה הוא חובהחלק מהפתרון לבעיות כאלה. נראה זאת בעצמנו בדוגמאות שלהלן.)

דוגמה 2

כאן, נוספו לעומס מודולים שנואים על ידי רבים, אך גם עלינו לשלב הבא.) מכיוון שהבעיה שוב עוסקת בשורש בודד, בואו נחפש אי-ווריאציות. אנו שמים לב ש-x נמצא בכל מקום בתוך פונקציות זוגיות - או מתחת למודול, או בריבוע.

בהירות מתחננת. כלומר, חוסר שונות תחת x ו-x.)

ובכן, עם x2הכל ברור - כאן השוויון ברור. אבל עם סכום המודולים בצד ימין, הכל לא כל כך ברור. בואו ננסה את הביטוי

במקום "x" תחליף את "מינוס x" ותראה מה קורה:

כפי שאתה יודע, המודול הוא גם פונקציה שווה ו"שורף" את המינוס:

אז מה אנחנו רואים? אנו רואים שמהחלפת x ב-x, גם הצד הימני של המשוואה לא השתנה(רק המודולים מוחלפים :)). וזה אומר שהמשוואה היא באמת בלתי משתנה מתחת ל-x ו--x. ואם יש לו איזה שורש x 0, אז מספר -x 0באופן אוטומטי יהיה גם השורשהמשוואה הזו.

לכן, לייחוד, שני השורשים הללו חייבים לַחפוֹף, כלומר יש צורך למלא את התנאי

אז אם למשוואה הזו יש שורש בודד, הוא יכול להיות רק אפס. נחליף את המספר 0 במשוואה המקורית במקום x:

להפשטות נוספות, אנו משתמשים בשוויון של הריבוע והמודלוס:

הבה נשכתב את המשוואה שלנו עם העובדות הבאות:

אנו מוציאים מודול אחד מהסוגר:

אז מתקבלים שלושה מועמדים לתשובה. עם ערכי הפרמטרים האלה אהמשוואה המקורית חייב להיות אחד מהשורשים שלו מספר 0. אבל האם המספר 0 שורש בודדאו לא, אנחנו צריכים לבדוק עכשיו. כעת אנו בודקים את הספיקות: אנו מארגנים מבחר תחרותי עבור המועמדים שלנו. :)

הסדר לא משנה כאן. נתחיל בארבעה: a = 4. אנחנו מחליפים במקום אלתוך המשוואה המקורית ארבע:

כל הארבע צומצמו בהצלחה ונשארו רק:

x 2 = |x| + |x|אוֹ x 2 - 2|x| = 0

אנחנו מחליפים שוב x2עַל |x| 2והוציאו מודול אחד מהסוגר:

המכפלה שווה לאפס כאשר לפחות אחד מהגורמים שווה לאפס:

אז מה אנחנו רואים? אנחנו רואים את זה ב a = 4יש למשוואה שלנו לא רק השורש x=0 , אבל גם שני שורשים נוספים- שניים ומינוס שניים! מה זה אומר? על מה ב a = 4יש למשוואה יותר משורש אחד (כלומר, עד שלושה). אז המועמד הראשון a = 4הליהוק שלנו לא עבר, אז הוא עף מהמאבק הנוסף בחבטה ולא מגיב. :)

השרביט מועבר למבקש הבא a = 6. נחליף את השישה במשוואה שלנו במקום הפרמטר א. אנחנו מקבלים:

השגנו משוואה טיפוסית עם מודולים, שנפתרת על ידי הרחבת המודולים במרווחים. ההנחה היא שאנשים שמתעניינים בבעיות לא סטנדרטיות עם פרמטרים כבר יודעים לפתור משוואות כאלה, אז כאן אשמיט תיאור מפורטפתרון המשוואה הזו (מה, איך, למה ולמה) ולסדר אותה בצורה תמציתית למדי.

כרגיל, אנו מחלקים את הציר המספרי למרווחים, שגבולותיהם הם האפסים של ביטויי תת-מודולים. במקרה שלנו, אלו הם 2 ו-2.

בואו נפתח את המודולים בכל מרווח ולמען הבהירות, נחתום אותם באיור.

1) x ≤ -2 . שני המודולים מורחבים עם סימן מינוס:

אז יש לנו את הדברים הבאים:

ברור שהצד השמאלי חיובי עבור כל x, מה שאומר שלמשוואה זו אין שורשים אמיתיים. אז, על המרווח (-∞; -2] למשוואה שלנו אין שורשים.

2) -2 < x < 2 . במקרה זה, המודול הראשון עדיין מורחב עם מינוס, אך המודול השני מורחב עם פלוס:

במקרה זה, המשוואה שלנו הופכת:

אפס שייך למרווח הנחשב (-2; 2) ולכן הוא השורש הראשון של המשוואה שלנו.

ולבסוף, המקרה השלישי הוא הבא.

3) x ≥ 2 . במקרה זה, שני המודולים מורחבים עם יתרון:

לאחר מכן

ברור שהצד השמאלי תמיד חיובי, ומכאן, כמו במקרה הראשון, השורשים ב x ≥ 2 גם המשוואה שלנו לא.

אז, כל המקרים מסודרים, והשורש היחיד של המשוואה שלנו הוא x=0.

ועכשיו אנחנו נזכרים שקיבלנו את המשוואה הזו ופתרנו אותה a = 6. וזה אומר שבשעה a = 6 המשוואה המקוריתבאמת יש היחידהשורש x = 0, ואין לו שורשים אחרים מלבד אפס (זה עתה הוכחנו זאת). את כל, a = 6אנחנו לגמרי מרוצים, והשישה הלכו ישר בתגובה.)

השלישי הלך!) תחליף עכשיו a = 2:

מוּעֲמָד a = 2ניתן להעסיק באופן מיידי בתגובה מבלי לראיין מראש את פתרון המשוואה המתקבלת. למה? אבל מכיוון שאם אתה מסתכל על המשוואה המתקבלת, אתה יכול לראות שהיא שונה מהמשוואה שהתקבלה עבור a = 6רק לפי סדר התנאים בצד ימין. כלומר, בעצם שום דבר.) וכמובן, יש לו גם את המספר 0 כשורש הייחודי שלו.

כך, a = 2מתאים גם.)

הכל, המשימה נפתרה לחלוטין! :)

תשובה: a = 2; a = 6.

אז, עם המשוואות פחות או יותר מתורגלות. עוברים לשלב הבא ועוברים למערכות עכשיו.)

דוגמה 3

"אז, אדוני... מודול, טריגונומטריה - הכל מעורב בערמה אחת, וזה איכשהו לא מאוד מעודד. אפשר כמובן לבטא ישירות מהמשוואה הראשונה y

ותחליף בשני, רק מה זה ייתן? הרי גם את כל הזבל הזה צריך לריבוע!

אז בסדר. כעת נחליף את כל הזבל הזה במשוואה השנייה במקום "ריבוע y":

ומה אפשר לעשות כאן? הו אבא! כן, הנה העיקר זהות טריגונומטרית sin 2 x + cos 2 x = 1, שניתן לבטל עם אחד בצד ימין.)

שְׂרִידִים:

נו, אז מה? אתה יכול לפרק את הצד השמאלי על ידי שליחת, למשל, אחד מהסוגריים לסוגריים (השפה הרוסית תסלח לי על הטאוטולוגיה). אבל משהו מתברר כמבלבל עד כאב... זו לא עובדה שאפשר יהיה להגיע לאמת, זו לא עובדה בכלל... תפסיקו! אבל אנחנו מדברים על הפתרון היחיד! או שאולי יש כאן גם משהו סימטרי או בלתי משתנה, שיקל בהרבה על הפתרון?

כשמסתכלים קצת על המערכת, אפשר שוב להבחין ש-x מסתובב בכל מקום בתוך פונקציות אפילו - מודולו, קוסינוס, סינוס בריבוע ... .

וזה אומר שיחד עם זוג כלשהו (x 0 ; y 0) המערכת הזו תהיה אוטומטית כפתרון שלה וזוג (-x 0 ; y 0). מה, לפי דרישת הייחודיות של הפתרון, אומר זאת

קיבל שניים נחוץערכי פרמטרים א. נחוץ בשביל מה? כדי זוג מספרים (0; y 0 ) היה הפתרון למערכת שלנו . ולא יותר. כמה מההחלטות הללו יתבררו בפועל עדיין לא ברור. ובכן, אנו בודקים שוב את המועמדים שלנו, ומחליפים כל אחד מהם במערכת המקורית.)

אז בואו נבדוק a = 0.

ובכן, מה אתה רואה כאן? ניתן לראות כי המשוואה השנייה, לאחר החלפה לתוכה y = -cos xמהמשוואה הראשונה, הפך בהצלחה ל זהות טריגונומטרית בסיסית, מה שנכון לגבי כלערכי x. מה זה אומר? כן! למערכת יש אין סוף פתרונות: לא משנה איזה x ניקח, תמיד ניתן יהיה לקבוע את ה-y מהמשוואה הראשונה, והמשוואה השנייה תתבצע אוטומטית. זה אומר שבשעה a = 0למערכת שלנו יש אין סוף פתרונות. זה, a = 0אותנו ברור לא מרוצה. אנו דוחים את המועמד הזה.)

הלקוח הבא, a = 2.

זה כבר כל כך קל לא לצאת מכאן (והזהרתי שבדיקת הספיקות היא לעתים קרובות ביותר חלק קשהפתרון בעיות). כגון מצבים לא סטנדרטיים, כאשר יש כמה מבנים הטרוגניים (ובדרך כלל מוגבלים) במשוואה משמאל ומימין (במקרה שלנו, זה המודולוס והקוסינוס), הנפוץ ביותר שיטת הערכהאו, יותר מדעית ויפה, שיטה מרכזית. ובכן, בואו ננסה להעריך כל אחת מהמשוואות.

ובכן, ראשית, אנחנו יודעים על המודול שהוא תמיד לא שלילי:

אז לגבי הצד השמאלי של המשוואה הראשונה, נוכל לומר את הדברים הבאים:

אז הצד השמאלי של המשוואה הראשונה הוא בכל מקרה לפחות שתיים.

מה עוד אפשר להעריך במשוואה הראשונה? ובכן ברור קוסינוס:

.

והנה כל הצד הימניאנחנו עדיין לא יכולים להעריך את המשוואה הראשונה: עדיין אין לנו שום הגבלה על ה-y. כלום, נקבל את זה עכשיו.)

כדי לעשות זאת, עבור למשוואה השנייה:

אנחנו מסתכלים עליו ומעמידים פנים: משמאל נמצא סכום של ריבועים- שתיים לא שליליתנאים. וסכום הריבועים הזה נותן אחד.

עכשיו בואו נחשוב: מה הם השניים לא שליליהאם מספרים יכולים להסתכם באחד? כפי שאתה יכול לנחש, אלה יכולים להיות כמה שברים מאפס לאחד (לדוגמה, 0.5 או 1/3), או כאשר אחד מהמונחים הוא אפס בדיוק, והשני הוא בדיוק אחד. אז בכל מקרה

0 ≤ sin 2 x ≤ 1ו 0 ≤ y 2 ≤ 1.

פַּעַם 0 ≤ y 2 ≤ 1, אז אנחנו יכולים לומר על השחקן עצמו את זה -1 ≤ y ≤ 1.

אז, קבענו מגבלות על קוסינוס ועל y. הם:

-1 ≤ כי x ≤ 1 ;

-1 ≤ y ≤ 1.

וזה אומר שהם סְכוּם(כלומר כל הצד הימני של המשוואה הראשונה) מוגבל כך:

-2 ≤ y + cos x ≤ 2.

כעת נסתכל על המשוואה הראשונה של המערכת

והגבולות שלנו.

עבור הצד השמאלי: 2(|x|+1) ≥ 2, כלומר צד שמאל לא פחות צמדים.

לצד ימין:-2 ≤ y + cos x ≤ 2, כלומר חלק ימין לא יותר צמדים.

מתי לדעתך השוויון של שני הצדדים של המשוואה אפשרי? כן! כאשר כל אחד מהם בּוֹ זְמַנִיתבְּדִיוּק שווה שניים!

המשמעות היא שהמשוואה הראשונה של המערכת מתפרקת לשני תנאים:

יחד עם המשוואה השנייה של המערכת, נקבל:

קל לאמת את זה (וזה די פשוט). היחידהפתרון של מערכת זו (ומכאן המקורית) הוא זוג מספרים (0; 1). זה אומר שערך הפרמטר a = 2אנחנו מרוצים לחלוטין. הכל, הבעיה נפתרה לחלוטין, אתה יכול לרשום את התשובה הסופית.

תשובה: a = 2.

אגב, שיטת ההחלפה הסטנדרטית (חושבים בכחול ממש בתחילת פתרון הדוגמה הזו), אותה קטענו, נמצאת כאן בחריקה, אבל היא גם עובדת. למעוניינים, נסו להשלים את הפתרון ע"י המשך הפירוק לגורמים ומשווה כל אחד לאפס. :) אבל הדוגמה הבאה תהיה הרבה יותר רצינית.

דוגמה 4

כבר במבט ראשון על המערכת, ברור ששום דבר לא משתנה בשום מקום, המשתנים לא באים לידי ביטוי "יפה" זה דרך זה - גם לא yדרך איקס, ולא איקסדרך y. אז, הטריקים הסטנדרטיים לא מתגלגלים. אבל! המשתנה x שוב עומד בכל מקום מתחת למודול או בריבוע, כלומר. תחת אפילו פונקציות! וזה אומר את זה היחידהפתרון של מערכת זו יכול להיות רק זוג מהצורה (0; y 0) . למה זה כך, אני חושב, כבר אין צורך להסביר.) אם זה עדיין לא ברור, תסתכל לפחות פעם נוספת לפחות בדוגמה הקודמת.

כאשר מחליפים x = 0, כל המערכת התרמו-גרעינית שלנו מפושטת מאוד:

אם y=1, אז: אם y = -1, זה:

3 = 5 1 - 5a 3 = 5 (-1) - 5א

5a = 2 5a=-8

a = 2/5 a = -8/5

אז, המועמדים שלנו הם שתי חמישיות ומינוס שמונה חמישיות. רק שניים.) אלו הם הערכים הדרושים של הפרמטר " א» בשביל זה, לזוג (0;y) היה אחד הפתרונות של המערכת המקורית. כעת, כרגיל, אנו בודקים את הספיקות, כלומר. כך שהזוג שלנו (0;y)לא היה רק ​​אחד מהפתרונות של המערכת, אלא היחידההחלטה שלה.

בוא נלך, נחליף את a = 2/5 לתוך המערכת. במקרה זה, המערכת כולה תקבל את הצורה:

במשוואה הראשונה, ראשית, צמצמתי את השניים, ושנית, אספתי את כל האיברים עם החמישה משמאל, ועם השלושה מימין. למה - זה יתברר בהמשך.)

"יש לנו מערכת נוראית מולנו, שאיכשהו צריכה להיות לְהַחלִיט. ליתר דיוק, לא כל כך להחליט, אלא לברר בדיוק כמה פתרונות יש לה - היחיד או לא. או אולי אין לזה פתרונות בכלל.) אבל יש בעיה אחת. איך לגשת אליה?

אם מתבטאים באופן מסורתי yדרך איקסמהמשוואה השנייה, אם כן

ואז מה לעשות עם הפלוס/מינוס הזה?! לא ברור…

ואם נביע את ה-y מהמשוואה הראשונה? ואז הסיוט יתברר:

ואם x עד y מהשנייה? זו גם לא מזרקה. אז, ברור שהשיטות הסטנדרטיות לא עובדות כאן. אז... אבל בשתי המשוואות שלנו יש מודולים ומרובעים - קונסטרוקציות מוגבלות (מלמטה). אבל מה אם ננסה להעריך את הצד השמאלי והימני של המשוואה הראשונה (הנוראה ביותר)?

מחשבות אמיתיות! אז המטרה שלנו היא הרגע הזה- להעריך את שני חלקי המשוואה הראשונה. הדקו את החגורות במכנסיים, כי עכשיו אנחנו צריכים להחליט אי שוויון רבים. ליתר דיוק, לא כל כך להחליט אלא לכתוב אותם, להוסיף, לשנות וכו'. אז, לפני שאנחנו מעריכים את המשוואה הראשונה:

אבל ראשית, בואו נסתכל על המשוואה השנייה:

שוב, כמו ב דוגמה 3, אנו רואים את סכום הריבועים השווים לאחד. מה זה אומר? זֶה כל אחד מהריבועים הללו בפני עצמו אינו עולה על 1.

זה, 0 ≤ x2 ≤ 1 ו 0 ≤ y2 ≤ 1 .

אותו הדבר ניתן לומר על המודולים x ו-y:

0 ≤ |x|≤ 1 ו 0 ≤ |y|≤ 1 .

לכן, בערך עצמם איקסו y ניתן לומר זאת -1 ≤ x ≤ 1 ו -1 ≤ y ≤ 1 .

ועכשיו, באמצעות אי השוויון הללו, אנו מעריכים את הצד השמאלי של המשוואה הראשונה, שווה ל סכום הביטויים 5 2 |x| ו-5 שנים:

פַּעַם 0 ≤ |x| ≤ 1 , ואז 2 0 ≤ 2 |x| ≤ 2 1 אוֹ 1 ≤ 2 |x| ≤ 2 .

כאן השתמשנו בהגדלה המונוטונית של הפונקציה f(x) = 2 x.

אם כעת כל שלושת החלקים של אי השוויון האחרון מוכפלים ב-5, נקבל:

2 ≤ 5 2 |x| ≤ 10

-1 ≤ 5 שנים ≤ 1

ולכן

-5 ≤ -5y ≤ 5 .

אולי לא ברור למישהו איך בדיוק מהאי-שוויון -1 ≤ 5 שנים ≤ 1 קיבל את אי השוויון -1 ≤ -5y ≤ 1 . אני מסביר.

-1 ≤ 5 שנים ≤ 1 |·(-1) (כפל את שני החלקים ב-1);

1 ≥ -5 שנים ≥ -1 (את כלהסימנים הפוכים)

-5 ≤ -5y ≤ 5 (אנחנו משכתבים את אי השוויון בצורה הרגילה).

את כל!

אז הגדרנו את גבולות הביטוי ל-5 2 |x| ו-5y:

2 ≤ 5 2 |x| ≤ 10

-5 ≤ -5y ≤ 5

כעת, כשמסכמים את שני אי השוויון הללו מונח אחר מונח, אנו מקבלים הגבלה על כל הצד השמאלי בכללותו:

בואו נזכור עובדה זו.) בואו נפנה כעת לצד הימני של המשוואה: 3x 2 - 3|x|.

אבל אנחנו נעריך את זה קצת אחרת.

כפי שכבר קבענו, 0 ≤ x2 ≤ 1 .

x2 ≤ |x| בְּ- 0 ≤ |x|≤ 1 .

מאיפה הבאתי את זה? איך הקוסם שלף את זה מהשרוול שלו?)

כדי להבין מדוע זה כך, בואו נצייר גרפים של המודול ("פינה") ושל פרבולות y \u003d x 2. על הקטע [-1; 1] התמונה תיראה כך:

ניתן לראות שעל הקטע [-1; 1] ה"פינה" נמצאת בכל מקום פרט לנקודות 0 ו-±1גבוה יותרפרבולות.

כך, x2 ≤ |x| בְּ- 0 ≤ |x|≤ 1 .

לאחר מכן x 2 - |x| ≤ 0 (רק העברתי את המודול שמאלה).

אז אם אי השוויון הזה מוכפל ב-3, נקבל:

לפיכך, כל הצד הימני לא יותר מאפס.

ועכשיו אנחנו זוכרים מה יש לנו עם הצד השמאלי:

אז צד שמאל לא פחות מאפס.

אומר, שוויוןחלק שמאל וימין אפשרי רק במקרה אחד - מתי כל אחד מהם בנפרד שווה לאפס :

בואו נפתור את המערכת הזו.

מכאן נקבל בקלות שלושה זוגות: (0; 1), (-1; 2), (1; 2).

עם זאת, הפתרונות של מערכת זו הם למעשה רק פתרונות המשוואה הראשונההמערכת הגלובלית שלנו.) זכור את המשוואה השנייה שלה: x2 + y2 = 1.

קל לראות שמתוך שלושת הזוגות הללו, רק הזוג (0; 1) מספק אותו. ומה זה אומר? בטבע הפראי של חישובים ונימוקים ארוכים, מבלי משים, אתה שוכח מהשאלה העיקרית...) כן! בְּ a = 2/5המערכת המקורית שלנו היא אכן יש את הפתרון היחיד.

את כל, a = 2/5 מוקף בעיגול כחלק מהתשובה.)

מה לגבי a = -8/5? אין מה לעשות, אנחנו מחליפים את זה במערכת שלנו:

אבל כאן כבר אי אפשר לעשות הערכה כל כך יפה: העשרה מימין קלקלו ​​הכל. (מה לעשות? יותר מפתרון אחד.) איך לנחש? ובכן, הכל תלוי במשימה הספציפית. וקצת מאינטואיציה ולפעמים ממזל. במקרה שלנו, בואו ננסה לתפוס את המשוואה השנייה:

x2 + y2 = 1.

בואו נסתמך על ההומניזם של המהדרים של המשימה ונתחיל מהפשוט ביותר - בואו נחפש כמה כֹּלפתרונות של משוואה זו והחליפו אותם בראשון. יש מעט מאוד מהם. ובכן, למשל, (1; 0):

מה עוד אפשר לבדוק? הא! יש לנו סימטריה X! פשוט השתמשנו בעובדה זו כדי לפתור את כל הבעיה! ואתה לא צריך לחשוב - הפתרון צץ מיד (-1; 0)!

את כל! בחרנו שניים שוניםפתרון של המערכת, כלומר הערך השני של הפרמטר a = -8/5לָנוּ בהחלט לא מרוצה. זהו, המשימה נפתרה! :)

תשובה: a = 2/5.

ובכן, כבר צברנו מספיק ניסיון כדי לשקול איזה פח כנה. אנחנו לוקחים את השור בקרניו! :)

דוגמה 5

אנחנו לא מפחדים מכלום ומנסים לחשוב ככה כשאנחנו רואים מפלצות כאלה:

"וואו, הם פישלו, זוועה! שורש, טנגנס, סינוס... אי אפשר להחליט בוודאות... אז תפסיקו! הם רוצים למצוא אותנו הדבר היחידפִּתָרוֹן. אז, סביר להניח, אנו מתבקשים למצוא איזו בנייה בלתי משתנה ולהשתמש בה כדי לפתור את כל הבעיה.

מה הכי בולט פה? ובכן, ראשית, במשוואה השנייה והשלישית מסתובבים בכל מקום xyו x+y, ומסידור מחדש של גורמים (מונחים) התוצאה לא משתנה. זה לא מקרי.) אז, אפילו כאן, בתוך הקוסינוס, ההבדל x-y, אשר, מהשינוי של x ו-y, ישנה סימן במקומות:

y-x = -(x-y).

רע... חכה שנייה! אבל הקוסינוס הוא פונקציה אחידה ושורף את המינוס! הכל בסדר, שום דבר לא ישתנה מתחת לקוסינוס!)

אבל יש גם את המשוואה הראשונה. עד כה, אין לו ריח של איווריות כלשהי ביחס לתמורה של x ו-y. ופתאום, אפשר לחשוף את השונות הזו גם שם? ובכן, בוא נראה...

ומה אפשר לעשות כאן? אתה יכול לפחות להרחיב את כל הסוגריים:

מכניס הכל למשוואה:

נראה שמשהו כבר בפתח:

ובכן, הנה מה שחיפשנו: x2+y2ו x+y הם מבנים בלתי משתנה. לגבי החלפה איקסעַל yו yעַל איקס. הידד!"

אז, המערכת כולה אינה משתנית בהחלפת x ב-y (ולהיפך). זה אומר שאם איזו משולשת של מספרים (x; y; z) היא הפתרון למערכת המרושעת הזו, אז אוטומטית ומשולש (y; x; z)יהיה גם הפתרון שלה! והייחוד של הפתרון של המערכת אפשרי רק כאשראיקס = y. עכשיו אתה יכול בכלהמערכת באומץ לא לכלול את y, מחליף אותו ב-x: xyיהפוך ל x2, x+y יהפוך ל-2x. ובכן, וכן הלאה.)

אז, המערכת הפכה קצת יותר פשוטה, אבל עדיין די מסורבל. אבל... משתנה זמסתובב בכל מקום תחת פונקציות זוגיות - או בריבוע, או בתוך סינוס בריבוע. וזה אומר שייחוד הפתרון אפשרי רק כאשר z = 0 . נִפלָא! אנו מחליפים אפס בכל מקום ב-z, וכל המערכת הנוראה שלנו תהיה פשוטה עוד יותר ותראה כך:

זה ברור מיד מהמשוואה השנייה x = 0. המשוואה השלישית עבור x = 0ברור שהוא מרוצה. ומהמשוואה הראשונה ב x = 0אנחנו מקבלים:

2a + 4 = 0,איפה a = -2.

וואו, כמה מעניין! התקבל ערך פרמטר אחד חוקי אחד. מינוס שתיים. אבל זה מוקדם מדי לשמוח, כי. זו עדיין לא תשובה: אנחנו עדיין צריכים לבדוק את הספיקות (כן, כן!). אין לאן ללכת, אנחנו מחליפים את ה-minus deuce במערכת המקורית במקום "a":

אנו מפשטים כל אחת מהמשוואות למקסימום. בראשון, נפתח את כל הסוגריים:

במשוואה השנייה, האיבר הנורא ביותר עם השורש מאופס בבטחה לאפס, השניים שנותרו מהסוגר הראשון מצטמצמים, ורק

ובכן, בואו נשאיר את המשוואה השלישית ללא שינוי. סה"כ:

ועכשיו אנחנו עושים קליפה כזו עם האוזניים - אנחנו מחליפים לתוך המשוואה הראשונה במקום x+yביטוי 2sin2zמהשני. מה נקבל:

בואו ננתח את המשוואה שהתקבלה. למה זה מדהים? זה משמאל הוא סכום של כמה ריבועים, כלומר. לא שליליתנאים! מתי אפשר אפס? סכומים של מונחים לא שליליים ? רק במקרה אחד בודד - מתי יחד עם זאת, כל איבר שווה לאפס ! זה:

אז, הפתרון היחיד למשוואה הראשונה הוא משולש המספרים (0; 0; 0). בואו נבדוק את השלישייה הזו עם שאר המשוואות: מה אם זה לא יעבוד שם? אז התשובה היא ללא ספק הסט הריק.)

כל השוויון מרוצים. לפיכך, הוכחנו זאת במלואה a = -2למערכת שלנו יש באמת פתרון ייחודי, והפתרון הזה הוא "שלוש סופגניות", כלומר. (0; 0; 0).

זה הכל! :)

תשובה: a = -2.

כמובן, חמש הדוגמאות הללו הנחשבות בשום פנים ואופן לא ממצות את כל מגוון הבעיות הפרמטריות לפתרון ייחודי ואינווריות.) אבל בהן ניסיתי לתאר בפירוט ובאופן מובן ככל האפשר כיצד לפעול במצב אם, פתאום, איפשהו (בבודק או ב-USE אמיתי) נתקלת בבעיה דומה. אז בואו נסכם את הנושא:

1) ברגע שאנו רואים את הביטוי "השורש היחיד / הפתרון היחיד" - אנו מנסים לחפש קונסטרוקציות בלתי משתנות או להגיע לאלו על ידי טרנספורמציות מקדימות. לרוב זו זוגיות, סימטריה ביחס למספר כלשהו , או ביחס לתמורות (החלפות) של משתנים או ביטויים.

2) לאחר שחשפנו את סוג האינווריות, אנו מחברים נחוץ תנאי לייחודיות של הפתרון ולחפש ערכים קבילים (הכרחיים) של הפרמטר. ככלל, כל המשימה פשוטה מאוד, והחיפוש שלהם לא קשה.

3) בדוק את ערכי הפרמטרים החוקיים שנמצאו לספיקות . אם לא ניתן לפתור את הבעיה הנובעת בשיטות סטנדרטיות, אנו משתמשים בטכניקות מיוחדות - מוגבלות, מונוטוניות וכו'. אם הם לא עוזרים, אנחנו מנסים למצוא את השורש או הפתרון. לרוב הם שוכבים על פני השטח, וככלל, הם מספרים שלמים.

4) אנחנו לא מפחדים. מנסה אפשרויות שונות.) ואנחנו מתאמנים יותר.) זו הדרך היחידה לפתח את הניסיון הדרוש בפתרון בעיות כאלה (ואכן כל) עם פרמטרים.

בהצלחה לכולם ולהתראות בקרוב!

השיטה השנייה של דגימת מסננים אנלוגיים נקראת השיטה של ​​טרנספורמציה בלתי משתנה של תגובת הדחף. תכונה ייחודיתשל שיטה זו היא שתגובת הדחף הדגימה של המסנן האנלוגי המתאים משמשת כתגובת הדחף של המסנן הדיגיטלי המחושב. כתוצאה מכך, תגובת התדר של המסנן הדיגיטלי נוצרת על ידי שכבת-על של תגובת התדר של המסנן האנלוגי הנדגם.

על מנת להדגים את שיטת הדגימה של מסנן אנלוגי באמצעות טרנספורמציה בלתי משתנה של תגובת הדחף שלו, אנו מפרקים את פונקציית ההעברה של מסנן זה (4.19) לשברים פשוטים:

, (4.45)

כאשר כל מקדם קובע את מיקום הקוטב ה-th. בכתיבת הרחבה (4.44) הונח שסדר המונה קטן מסדר המכנה ושכל הקטבים פשוטים. ההנחה ש, חייבת להתקיים עבור מסנן מדוגם, כי אחרת הכינוי בתגובת התדר של המסנן הדיגיטלי יהפוך לבלתי חוקי. אם לא כל הקטבים פשוטים, אז יש לשנות מעט את התוצאות שיתקבלו בסעיף זה.

תגובת הדחף של מסנן אנלוגי עם פונקציית העברה של הצורה (4.44) מתוארת על ידי היחס

. (4.46)

תוך דיסקרטציה, אנו מקבלים את תגובת הדחף של המסנן הדיגיטלי

(4.47)

היכן תקופת הדגימה. מצא את ה-Z-טרנספורמציה שלו

(4.48)

על ידי שינוי סדר הסיכום וסיכום מעל , אנו מקבלים

(4.49)

הבה נשווה נוסחאות (4.49) ו-(4.44). ניתן לראות כי עבור עמודים פשוטים, המעבר מ-to מתבצע באמצעות מיפוי המשתמש בתחליף

. (4.50)

אם הקטבים מורכבים, אז גם השאריות ב- (4.44) יהיו מורכבות. הפונקציה היא אמיתית, כך שהקוטב המצומד המורכב והשארית חייבים להתקיים. הבה נסכם את המונחים המצומדים המורכבים הללו ב-(4.44):

. (4.51)

לשים ו, ​​אנחנו מקבלים

. (4.52)

שימוש בהחלפת המיפוי (4.50) עבור כל איבר בנוסחה (4.51) נותן

. (4.54)

מנוסחאות (4.52) ו- (4.54) אנו מקבלים

(האינדקס מושמט כאן, והמונה מחולקים ב).

להלן שני מקרים מיוחדים שימושיים של החלפת מיפוי זו, המתאימים למסננים אנלוגיים עם תגובות דחפים ו:

צוין לעיל שתגובת התדר של מסנן דיגיטלי המחושב בשיטת הטרנספורמציה הבלתי משתנה של תגובת הדחף נוצרת על ידי הטלת תגובת התדר של המסנן האנלוגי הנדגם. כך אפשר לכתוב

, (4.58)

היכן הוא תדר הדגימה הזוויתי של המסנן הדיגיטלי.

תאנה. 4.7. מיפוי ממטוס s ל G-מישור לשיטה של ​​טרנספורמציה בלתי משתנה של תגובת הדחף.

באיור. 4.7 הראה את המיפוי ממישור s למישור z המקביל לטרנספורמציה הבלתי משתנה של תגובת הדחף. כל פס רוחב אופקי מהמישור-ממפה למישור z. לכן, כל הרצועות הסמוכות ממישור ה-s יחפפו זו את זו במישור ה-z כשהן מוצגות. מכאן נובע שכדי שתגובות התדר של המסנן האנלוגי המקורי ותגובת האימפולס של המסנן הדיגיטלי המחושב בשיטת הטרנספורמציה הבלתי משתנה יתאימו זה לזה, יש צורך שפס המעבר של המסנן האנלוגי יהיה בטווח . כדי למלא תנאי זה, יש צורך להכניס מסנן נמוך מעבר נוסף לפני תחילת ההמרה, המבטיח הגבלה מתאימה של רוחב הפס של המסנן האנלוגי.

דוגמאטרנספורמציה בלתי משתנה של תגובת הדחף.כדי להמחיש שיטה זו, אנו מבססים מסנן אנלוגי עם פונקציית העברה של הטופס

שימוש ישיר בתחליף המיפוי (4.50) נותן

תאנה. 4.8. מאפייני משרעת ופאזה של המסנן האנלוגי.

תגובת התדר של מסנן אנלוגי ניתנת על ידי

.

באיור. 4.8 מציג את מאפייני המשרעת והפאזה של מסנן זה. מאפיינים של המסנן הדיגיטלי המתאים עבור ערכים שוניםתקופת הדגימה מוצגת באיור. 4.9. ברור שככל שקצב הדגימה יורד (כלומר, עולה) אפקטי הכינוי יכולים להיות זניחים ותגובות התדר של המסננים האנלוגיים והדיגיטליים הופכים דומים זה לזה.

שיטת אינווריאציה

שיטת האינווריאנס מורכבת מהעובדה שבמכשיר המדידה, בנוסף למעגל המדידה (ערוץ), קיים מעגל השוואתי (ערוץ) שלא מופעל עליו אות כניסה, אך הוא, כמו מעגל המדידה, מתחת ל- השפעה של כמות משפיעה כלשהי. יתרה מכך, הפרמטרים של המעגל ההשוואתי נבחרים כך שהשינוי באות שלו בהשפעת הכמות המשפיעה זהה לשינוי האות של מעגל המדידה בפעולת כמות זו, כלומר, ההפרעות הנגרמות על ידי כמות משפיעה נכנסת למכשיר המדידה דרך שני ערוצים (עקרון שני ערוצים). השימוש בהפרש בין האותות של מעגלי המדידה וההשוואה (כאשר מעגלים אלה מופעלים באופן דיפרנציאלי) מבטיח את עצמאות האות המתקבל מהכמות המשפיעה הנקראת, כלומר השיטה מבטיחה אי הכללה של שגיאה נוספת נגרם כתוצאה משינויים בחלק, ככלל, מהכמות המשפיעה העיקרית.

שיטת ריצה ישירה

שיטת המהלך קדימה מורכבת מכך שהאות הנמדד מסופק לאלמנט הרגיש של מכשיר המדידה באמצעות המפתח, בעזרתו מנותק האות הנמדד מעת לעת מהאלמנט הרגיש בזמן והאות, הערך של ששווה לאפס, מוחל על האחרון. זה מבטיח את פעולת מכשיר המדידה בענף העולה (ריצה קדימה) של המאפיין הסטטי עבור כל הערכים של האות הנמדד, מה שמבטל את השגיאה המשמעותית ביותר של מכשירי מדידה רבים - השגיאה משינוי.

שיטת מדידה עזר

השיטה של ​​מדידות עזר היא להפוך את תהליך ההתחשבות בשגיאה הנוספת של מכשיר המדידה לפי הפונקציות הידועות של השפעת מספר כמויות משפיעות. לשם כך, ערכי הכמויות הללו נמדדים, ובעזרת מכשיר מחשוב שנבנה תוך התחשבות בפונקציות ההשפעה הנקובות, אות הפלט של מכשיר המדידה מתוקן אוטומטית.

שיטת המרה הפוכה

שיטת ההמרה ההפוכה (שיטה איטרטיבית) מבוססת על שימוש, בנוסף למעגל המדידה הישירה (ממיר ישיר), בנוסף למכשיר המדידה, במעגל המסוגל להמיר הפוך את אות המוצא (ממיר הפוך), בעל דיוק גבוה משמעותית ממעגל ההמרה הישירה. תוצאת המדידה מתקבלת על ידי איטרציות. במהלך כל איטרציה מבוצעות ברצף: טרנספורמציה ישירה של הערך הנמדד ואחסון התוצאה, טרנספורמציה הפוכה של הערך המאוחסן של ערך זה, טרנספורמציה ישירה של אות הממיר ההפוכי התואמת לערך המאוחסן של הערך הנמדד, והשוואה. של תוצאות שתי התמורות הללו, שעל בסיסן נוצר אות מתקן. הממיר ההפוך בשיטה זו ממלא תפקיד של מידה רב ערכית, לפיה מתוקן המאפיין הסטטי של הממיר קדימה. שיטת הטרנספורמציה ההפוכה מאפשרת לצמצם, בהתאם לאלגוריתם התיקון בו נעשה שימוש, את השגיאות המתוספות והמכפילות של מכשירי המדידה.

תקציב עירוני מוסד חינוכיאולם התעמלות מספר 9

פרויקט ניסוי-סיכום

בנושא זה:

יישום שיטת האינווריאנטים בפתרון בעיות USE ובעיות אולימפיאדה

מְבוּצָע:

תלמיד XIמחלקה "B".

טישצ'נקו אלינה

יועץ מדעי:

מורה למתמטיקה

חטונטצבה

אירינה ולדימירובנה

וורונז' - 2017

תוֹכֶן

מבוא

במתמטיקה המודרנית תפקיד חשובמשחק את המושג אינווריאנטיות, כלומר. אי-שינוי של אובייקט מתמטי. הרבה מאוד הגדרות למתמטיקה קשורות למעשה למושג זה, אם כי המונח אינוריאנס עצמו אינו נמצא בספרי לימוד.

דוגמא: פונקציה אפילו f(x) עם תחום R אינו משתנה, כי f(x)=f(-x).

הנוכחות של תכונת אי-ווריאציה כזו או אחרת של אובייקט מתמטי מאפשרת לקבוע כמה מאפיינים איכותיים כלליים של אובייקט זה.

מטרת עבודה זו היא להראות את היישום של שיטת האינווריאנטים בפתרון בעיות USE ובעיות אולימפיאדה.

ספרות רבה מוקדשת לנושא זה על ידי הוצאות לאור של האוניברסיטאות המובילות במדינה, כגון אוניברסיטת מוסקבה והמכון לפיזיקה וטכנולוגיה של מוסקבה. הספר הקלאסי על תיאוריית האינווריאנטים הוא ספרה של המתמטיקאית הגרמנית המצטיינת הרלין וייל. והסטודנטים של אוניברסיטת אוקספורד מפרסמים את המגזין השנתי "The Invariant".

הנושא הזה נראה רלוונטי מאוד, כי. השיטה של ​​אינוריאנטים מקלה למדי על פתרון בעיות שלב מתקדםקשיים.

פרק 1. יישום השיטה האינוריאנטית בפתרון בעיות אולימפיאדה

זוגיות (אי-זוגי), שאר החלוקה, תמורה, צביעה וכו' נחשבים לרוב כאינוריאנטים.

השימוש בזוגיות הוא אחד הרעיונות הנפוצים ביותר בפתרון בעיות אולימפיאדה. הבה ננסח את ההצהרות החשובות ביותר שעליהן מבוסס היישום של רעיון זה:

השוויון של סכום מספר מספרים שלמים עולה בקנה אחד עם השוויון של מספר האיברים האי-זוגיים;

הסימן של המכפלה של מספר מספרים (חוץ מאפס) נקבע על פי הזוגיות של מספר הגורמים השליליים.

משימה 1.

יש עשרה פלוסים וחמישה עשר מינוסים כתובים על הלוח. מותר למחוק כל שני סימנים ולכתוב במקומם פלוס אם הם זהים, ומינוס אחרת. איזה שלט יישאר על הלוח לאחר ביצוע עשרים וארבע פעולות כאלה?

פִּתָרוֹן.

בואו נחליף כל פלוס במספר1 , וכל מינוס הוא מספר-1 .

לאחר מכן אנו מוחקים שני מספרים ורושמים את המוצר שלהם. לכן, המכפלה של כל המספרים הכתובים על הלוח יישאר ללא שינוי.

מכיוון שהמוצר היה שלילי בתחילה (15 מספרים שליליים), ואז בסוף זה יישארשלילי.

תשובה: מינוס.

משימה 2.

הילד קיבל שני עבור מִבְחָןבמתמטיקה ובהתקף ייאוש קרע את הנייר עם עבודתו לעשר חתיכות. לאחר מכן הוא קרע את אחת החתיכות שנוצרו ל-10 חתיכות נוספות. האם יכולים להיות פיסות נייר של 2015 בסוף ההרפיה?

פִּתָרוֹן.

בכל פעם פיסת נייר אחת נקרעת ל-10 חתיכות, הילד גדל סה"כפיסות נייר עד 9. אחרי הקרע הראשון יהיו לו 1+9=10 יח', אחרי השני - 10+9=19 יח' וכו'. כלומר, מספר פיסות הנייר על הקרע ה-n נמצא בנוסחה 1+9נ.

בוא נבדוק אם ניתן לייצג את המספר 2015 כ-1+9נ:

1+9 נ=2015;

9 נ=2014.

2014 אינו מתחלק ב-9 ללא שארית, לכן, 2015 חתיכות לאחר השלמת הרפיה לא יכול להיות.

תשובה: לא

משימה 3.

על הלוח כתובים מספרים מ-1 עד 1998. מותר למחוק כל שני מספרים במהלך אחד ולכתוב את ההפרש שלהם במקום עד שיישאר מספר אחד. האם מספר זה יכול להיות אפס?

פִּתָרוֹן.

שקול את סכום כל המספרים הכתובים על הלוח לפני ואחרי צעד אחד. בואו נמחק את המספריםא, ב. אז בהתחלה הסכום של כל המספרים היה שווה , ולאחר מכן , איפהסהוא הסכום של כל שאר המספרים. כפי שאתה יכול לראות, ההחלפה (א+ ב) על (א- ב) אינו משנה את השוויון של סכום כל המספרים. סכום המספרים ממש בהתחלה הוא מספר אי-זוגי (
), מה שאומר שבכל שלב סכום המספרים הכתובים על הלוח יהיה אי זוגי. אפס הוא מספר זוגי, אז אנחנו לא יכולים לקבל אותו על הלוח.

תשובה: לא.

משימה 4.

כל תא של השולחן המרובע 2*2 צבוע בשחור או צבע לבןכפי שמוצג באיור למטה. במהלך אחד, ניתן לצבוע מחדש את התאים בכל שורה, בכל עמודה או בכל אלכסון: תאים שחורים הם לבנים ותאים לבנים הם שחורים. האם ניתן לקבל טבלה בכמה מהלכים, שכל התאים בה לבנים?

פִּתָרוֹן.

שייך כל תא ל-1 אם הוא צבוע לבן, ו-1 אם הוא בצבע שחור. ואז שינוי הצבעים פירושו שינוי הסימנים. שקול את המכפלה של כל המספרים המתאימים לתאים. מכיוון שכאשר צובעים מחדש, אנו משנים את הסימנים של שני גורמים בדיוק, המכפלה של כל ארבעת המספרים לא משתנה. בהתחלה, מוצר זה שווה ל-1. הצביעה הנדרשת תואמת למוצר השווה ל- 1. לכן, אי אפשר לצבוע מחדש את הטבלה עם הפעולות המצוינות.

תשובה: לא.

משימה 5.

יש 1, 9 ו-98 אבנים בשלוש ערימות. בתנועה אחת מותר לקחת אבן אחת מכל שתי ערימות ולהעבירן לשלישית. האם ניתן לאסוף את כל האבנים באחת הערימות בכמה מהלכים?

פִּתָרוֹן.

קחו בחשבון את השאר כאשר מחלקים בשלושה מהמספרים המקוריים - מספר האבנים בערימות. בערימה הראשונה, היתרה היא 1, בשנייה - 0, בשלישית - 2. חשבו מה יקרה אחר כך מבחינת שאריות כאשר נעביר את האבנים:

מצאנו אינוריאנט - לאחר כל אחת מהפעולות, השאריות יהיו זהות: 0, 1, 2, רק שכבר מחולקים אחרת. אם נוכל לאסוף את כל האבנים בערימה אחת, אז השארית כאשר מחלקים ב-3 בכל הערימות תהיה זהה (שווה ל-0). לכן, אי אפשר לאסוף את כל האבנים בערימה אחת על ידי הפעולות המצוינות.

תשובה: לא.

משימה 6.

ניתן במישור קו מצולע סגור שאינו חוצה את עצמו, שאין שלושת הקודקודים שלו על אותו קו ישר. אנו קוראים לזוג קישורים שאינם שכנים קו שבורמיוחד, אם הרחבה של אחד מהם חותכת את השנייה. הוכח שמספר הזוגות המיוחדים הוא זוגי.

פִּתָרוֹן.

קח את הקישורים השכנים AB ו-BC והתקשרפינה זווית סימטרית לזווית ABC ביחס לנקודה B (הפינה מוצללת באיור למטה). ניתן לשקול אותן פינות עבור כל הקודקודים של הפוליליין. ברור שמספר הזוגות המיוחדים שווה למספר נקודות ההצטלבות של קישורים עם פינות. נותר לציין שמספר הקישורים של הפוליליין שמצטלבים עם פינה אחת הוא זוגי, שכן בדרך מ-A ל-C, הפוליליין נכנס לפינה כמה פעמים שהוא יוצא ממנה (הדבר נובע מהתנאי שלא מונחים שלושה קודקודים של הפוליליין על אותו קו). לכן, מספר הזוגות הבודדים הוא זוגי, מה שהיה צריך להוכיח.

משימה 7 (שלב אזורי של האולימפיאדה הכל-רוסית לתלמידי בית הספר, 2016-2017, כיתה י"א, יום ב', מס' 8).

בתחילה מונחים על השולחן 100 קלפים, שכל אחד מהם מכיל מספר טבעי; בעוד שביניהם בדיוק 28 קלפים עם מספרים אי-זוגיים. לאחר מכן, ההליך הבא מתבצע בכל דקה. על כל 12 קלפים על השולחן, מחשבים את מכפלת המספרים הכתובים עליהם, מחברים את כל המוצרים הללו, והמספר המתקבל נכתב על כרטיס חדש, שמתווסף לאלו השוכבים על השולחן. האם ניתן לבחור את 100 המספרים המקוריים בצורה כזו שלכל d טבעי, במוקדם או במאוחר יופיע קלף על השולחן עם מספר המתחלק ב
?

פִּתָרוֹן.

אם ברגע מסוים ישנם מספרים אי-זוגיים בדיוק בין המספרים בכרטיסים, אז בין התוצרים של מספרים ב-12 בדיוק
מוזר; לכן, המספר בקלף הבא שנוסף יהיה אי זוגי בדיוק כאשר הוא אי זוגי (ואז k יגדל ב-1 באותה דקה).

קל לראות שהמספר
מוזר (זה נובע מהעובדה שהכוחות של שניים הכלולים ב
ו
, שווים). יתר על כן, לאחר אימות עוקב, אנו משיגים את הראשון
,
,
הם מספרים אי-זוגיים, ו
- אפילו. לכן, כשמספר הקלפים האי-זוגיים יגיע ל-32, הוא לא יגדל יותר, ותמיד יהיו רק 32 קלפים אי-זוגיים על השולחן, וכל המספרים שנוספו יהיו זוגיים.

תמשיך עכשיו נשלב - סכום כל התוצרים של 12 מהמספרים הכתובים על הקלפים, ו הוא סכום כל המוצרים של 11 מספרים. מספר
, שייכתב בכרטיס הבא, שונה מ לפי סכום המוצרים של 12 מספרים, שביניהם יש מספר זוגי שזה עתה נוסף , כלומר עַל
. אומר, . מספר - זוגי, מאז מספר הסכומים האי-זוגיים של 11
אֲפִילוּ. אומר,
אי זוגי, והעוצמה המקסימלית של שניים שמפרידה
שווה לחזק המקסימלי של שניים שמתחלק . זה אומר שמאז בתחילה לא היו מספרים על השולחן כי עבור כל טבעידלחלק ב , אז מספרים כאלה לא יופיעו יותר.

תשובה: לא, אתה לא יכול.

פרק 2

לאחר ניתוח מספר גדולבעיות, הידור אלגוריתם לפתרון בעיות עם פרמטר בשיטת האינוריאנטים.

אלגוריתם לפתרון בעיות עם פרמטרים באמצעות אינוריאנט:

1) בדוק אם אין שוונות את המשוואה הנתונה, אי-שוויון, מערכת המשוואות (אי-שוויון);

2) למצוא ערכים קבילים של הפרמטר מבדיקת מילוי התנאים: במקרה של "סימטריה ביחס לסימן המשתנה", החלף את הערך האפס שלו; עם "סימטריה תחת תמורה של משתנים" כל המשתנים מסומנים באות אחת;

3) על ידי בדיקה כדי לוודא שהערכים שנמצאו של הפרמטר עומדים בתנאי הבעיה;

4) רשום את התשובה.

הצהרה 1 . אם הביטוי
בלתי משתנה תחת טרנספורמציות
ומשוואה
יש שורש ,זֶה

הצהרה 2. אם הביטוי

ומשוואה
יש פתרון
, ואז זוג מספרים

הצהרה 3 . אם הביטוי
בלתי משתנה תחת טרנספורמציה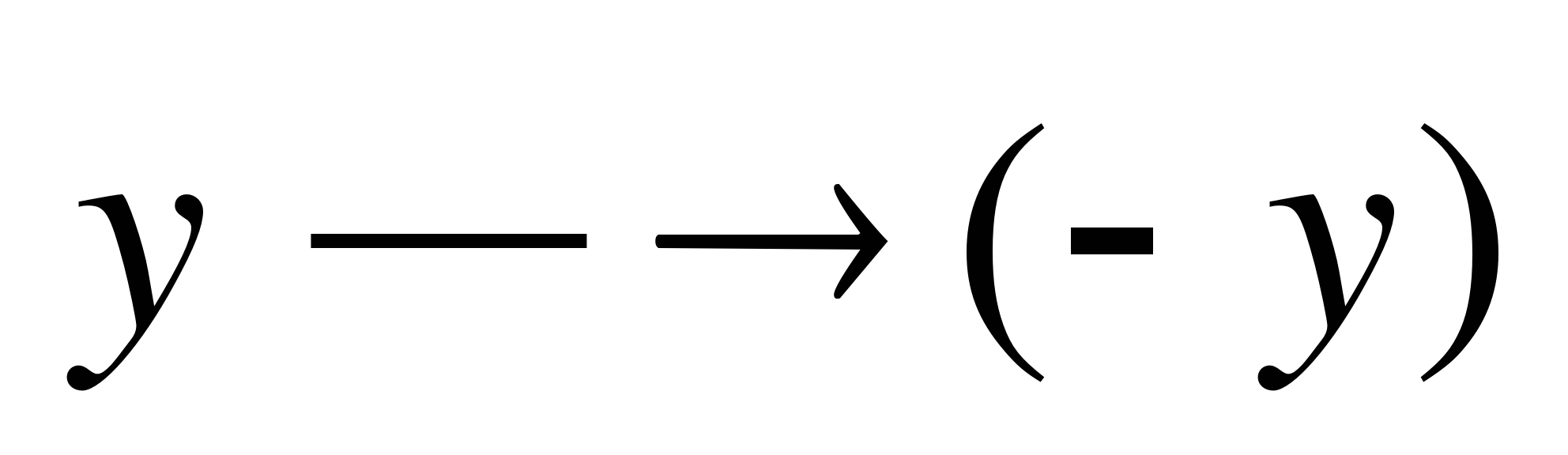
ומשוואה
יש פתרון
, ואז זוג מספרים
גם פתרון למשוואה הזו.

הצהרה 4. אם הביטוי
בלתי משתנה תחת טרנספורמציה
ו
, והמשוואה
יש פתרון
, ואז כמה מספרים
גם פתרון למשוואה הזו.

הצהרה 5. אם הביטוי
בלתי משתנה תחת טרנספורמציה
, המשוואה
יש שורש , זֶה
הוא גם השורש של המשוואה הזו.

משימה 1.

מצא את כל הערכים של הפרמטר a שלמשוואה יש פתרון אחד עבורו

פִּתָרוֹן.

שימו לב שאם הוא שורש המשוואה, אז - - גם שורש => שורש אחד יכול להיות רק אם =-=0.
תחליף
:

בְּ
:

שורש אחד, מתאים

בְּ
:

צד שמאלמשוואה זו גדולה או שווה ל
, והגבול התחתון הזה הוא מדויק - מגיעים אליו ב
. להעריך את הצד הימני קצת יותר קשה. קודם כל, נציין שכאשר משנים את המשתנה מ
לפני
ביטוי
משתנה בין -1 ל-1. על הקטע
פוּנקצִיָה
עולה מונוטונית מ
לפני
. לכן הביטוי
משתנה מ
לפני
. בהתאם לכך, הצד הימני של המשוואה (1) משתנה מ
לפני
, והערכים של הצד הימני של המשוואה ממלאים לחלוטין את הקטע הזה. מהמידע שהתקבל לגבי הערכים האפשריים של הצדדים השמאלי והימני של המשוואה (1), נובע שהם יכולים להיות שווים רק כאשר הם שווים בו זמנית
. במילים אחרות, משוואה (1) שווה ערך למערכת:

למשוואה הראשונה יש שורש בודד
, שגם עונה על המשוואה השנייה של המערכת. המשמעות היא שלמערכת, ואיתה המשוואה המקורית, יש פתרון ייחודי
. לכן, הערך המסומן של הפרמטר (
) חייב להיכלל בתגובת המשימה.

תשובה: 0;
.

משימה 2. מערכת אי שוויון
יש פתרון ייחודי?

פִּתָרוֹן. 1. במערכת זו אנו רואים "סימטריה ביחס לשינוי המשתנים". ואז, אם זה פתרון למערכת, אז
גם הפתרון של המערכת. הייחודיות של הפתרון מושגת בתנאי
(הצעה 4).

2. ציון כל המשתנים דרך
מאי שוויון שיש לו פתרון ייחודי, אם ההבחנה של טרינום ריבועי הוא אפס, הָהֵן.

3. בדוק אם למערכת יש פתרון ייחודי לערכים שנמצאו של הפרמטר.

א) תחליף ב המערכת הזאתאי שוויון
:

נוסיף את אי השוויון של המערכת האחרונה:
+

פתיחת הסוגריים והבאת מונחים כמו, נקבל:. מכאן



- רק החלטה.

ב) בעת החלפה
אנחנו מקבלים את הפתרון היחיד

תשובה:

משימה 3. מצא את כל הערכים של הפרמטר שעבורו מערכת המשוואות

יש ארבעה פתרונות שונים.

פִּתָרוֹן.

זה נובע מצורת המערכת כי > 0.

1. המערכת היא בלתי משתנה כשהיא מוחלפת ב- ו על - . לכן, אם הערך הרצוי של הפרמטר וזוג מספרים ;
הוא הפתרון של המערכת, ואז הזוגות
;
, ;
ו
; -
גם פתרונות מערכת. (הצעות 2 ו-3). לכן, אנו מוצאים פתרונות עבור ≥ 0, ≥0. בואו נצייר גרפים של משוואות במערכת קואורדינטות אחת. גרף של המשוואה הראשונה - נקודות של צלעות הריבועא ב ג ד, הגרף של השני הוא עיגול שמרכזו במקור וברדיוס שווה ל.

האיור מראה שלמערכת יש בדיוק ארבעה פתרונות בשני מקרים: 1)


;
; כי > 0, אם כן
; 2) = 0 ההוא רדיוס מעגל הכתוב בריבוע שצלעו שווה ל
לפי ט פיתגורס מהמשולש BOC.

אומר, 0E =
, אז =
איפה 2
= 2; 2 =
ו=
.

תשובה: = 1; =
.

משימה 4. באילו ערכים של הפרמטר מערכת משוואות
יש בדיוק שלושה פתרונות?

פִּתָרוֹן. 1. אם זוג מספרים ;
- פתרון המערכת, הוא הפרמטר הרצוי, ואז הזוג

; -
הוא גם הפתרון של המערכת. אומר, = -
= 0. (טענה 3).

2. מחליף = 0 לתוך מערכת המשוואות הנתונה.

אנחנו מקבלים:

הבה נבדוק האם יש למשוואה הנתונה עבור הערכים שנמצאו החלטה בלבד. בְּ =-3 יש לנו:

בואו נפתור את המשוואה השנייה של המערכת:

אוֹ
אין פתרונות.

אם y=0, אז x=5 ו-(-5; 0) הם הפתרון היחיד של המערכת. אומר,
לא מתאים.. סיכום

במהלך העבודה שנעשתה, שיטת האינווריאנטים נחקרה. שיטת האינווריאנטים יושמה בפתרון בעיות USE המכילות פרמטר, ובעיות אולימפיאדה לצביעה, זוגיות, שאריות חלוקה, מוצדקות ומוצגות בבירור שימוש מעשישיטה.

רשימת ספרות משומשת