תינתן פונקציה f, שבשלב מסוים ל-x 0 יש נגזרת סופית f (x 0). אז הקו העובר דרך הנקודה (x 0; f (x 0)), שיש לה שיפוע f '(x 0), נקרא משיק.
אבל מה קורה אם הנגזרת בנקודה x 0 לא קיימת? ישנן שתי אפשרויות:
- גם המשיק לגרף לא קיים. הדוגמה הקלאסית היא הפונקציה y = |x | בנקודה (0; 0).
- המשיק הופך אנכי. זה נכון, למשל, עבור הפונקציה y = arcsin x בנקודה (1; π /2).
משוואת טנג'נט
כל ישר לא אנכי ניתן על ידי משוואה בצורה y = kx + b, כאשר k הוא השיפוע. הטנגנס אינו יוצא מן הכלל, וכדי להרכיב את המשוואה שלו בנקודה כלשהי x 0, מספיק לדעת את ערך הפונקציה והנגזרת בנקודה זו.
אז תן לפונקציה y \u003d f (x), שיש לה נגזרת y \u003d f '(x) על הקטע. אז בכל נקודה x 0 ∈ (א; ב) ניתן לצייר משיק לגרף של פונקציה זו, שניתן במשוואה:
y \u003d f '(x 0) (x - x 0) + f (x 0)
כאן f '(x 0) הוא הערך של הנגזרת בנקודה x 0, ו-f (x 0) הוא הערך של הפונקציה עצמה.
מְשִׁימָה. נתונה פונקציה y = x 3 . כתבו משוואה למשיק לגרף של פונקציה זו בנקודה x 0 = 2.
משוואת טנג'נט: y \u003d f '(x 0) (x - x 0) + f (x 0). הנקודה x 0 = 2 ניתנת לנו, אך יש לחשב את הערכים f (x 0) ו-f '(x 0).
ראשית, בואו נמצא את הערך של הפונקציה. הכל קל כאן: f (x 0) = f (2) = 2 3 = 8;
עכשיו בואו נמצא את הנגזרת: f '(x) \u003d (x 3) ' \u003d 3x 2;
תחליף בנגזרת x 0 = 2: f '(x 0) = f '(2) = 3 2 2 = 12;
אז נקבל: y = 12 (x - 2) + 8 = 12x - 24 + 8 = 12x - 16.
זוהי משוואת המשיק.
מְשִׁימָה. חבר את משוואת המשיק לגרף של הפונקציה f (x) \u003d 2sin x + 5 בנקודה x 0 \u003d π / 2.
הפעם לא נתאר בפירוט כל פעולה – נציין רק את השלבים המרכזיים. יש לנו:
f (x 0) \u003d f (π / 2) \u003d 2sin (π / 2) + 5 \u003d 2 + 5 \u003d 7;
f '(x) \u003d (2sin x + 5) ' \u003d 2cos x;
f '(x 0) \u003d f '(π / 2) \u003d 2cos (π / 2) \u003d 0;
משוואת טנג'נט:
y = 0 (x − π /2) + 7 ⇒ y = 7
במקרה האחרון, הקו התברר כאופקי, כי השיפוע שלו k = 0. אין בזה שום דבר רע - פשוט נתקלנו בנקודת קיצון.
המאמר נותן הסבר מפורט על ההגדרות, המשמעות הגיאומטרית של הנגזרת עם סימון גרפי. משוואת הישר המשיק תיחשב עם דוגמאות, יימצאו משוואות המשיק לעיקולים מסדר 2.
Yandex.RTB R-A-339285-1 הגדרה 1
זווית הנטייה של הקו הישר y \u003d k x + b נקראת הזווית α, הנמדדת מהכיוון החיובי של ציר ה-x לקו הישר y \u003d k x + b בכיוון החיובי.
באיור, כיוון השור מצוין על ידי חץ ירוק וקשת ירוקה, וזווית הנטייה על ידי קשת אדומה. הקו הכחול מתייחס לקו ישר.
הגדרה 2
מִדרוֹןהישר y = k x + b נקרא המקדם המספרי k .
השיפוע שווה לשיפוע של הישר, במילים אחרות k = t g α .
- השיפוע של הישר הוא 0 רק כאשר o x מקביל והשיפוע שווה לאפס, כי הטנגנס של אפס הוא 0. אז, צורת המשוואה תהיה y = b.
- אם זווית הנטייה של הישר y = k x + b חדה, אז התנאים 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается מספר חיובי, כי הערך של המשיק עומד בתנאי t g α > 0, ויש עלייה בגרף.
- אם α \u003d π 2, אז המיקום של הקו הוא מאונך ל-x. השוויון מצוין על ידי השוויון x = c כאשר הערך c הוא מספר ממשי.
- אם זווית הנטייה של הישר y = k x + b קהה, אזי היא מתאימה לתנאים π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.
סקאנט הוא קו ישר העובר דרך 2 נקודות של הפונקציה f (x). במילים אחרות, סקנט הוא קו ישר שעובר דרך כל שתי נקודות בגרף. פונקציה נתונה.

האיור מראה ש-A B הוא גזרה, ו-f (x) הוא עקומה שחורה, α היא קשת אדומה, המציינת את זווית הנטייה של הגזרה.
כאשר השיפוע של ישר שווה לטנגנס של זווית הנטייה, ברור שניתן למצוא את המשיק ממשולש ישר זווית A B C ביחס לרגל הנגדית לזו הסמוכה.
הגדרה 4
נקבל את הנוסחה למציאת הססקנט של הטופס:
k = t g α = B C A C = f (x B) - f x A x B - x A , כאשר האבססיס של נקודות A ו-B הם הערכים x A , x B , ו- f (x A) , f (x ב) הם פונקציות הערכים בנקודות אלו.
ברור, שיפוע הסקאנט מוגדר באמצעות השוויון k \u003d f (x B) - f (x A) x B - x A או k \u003d f (x A) - f (x B) x A - x B, ויש לכתוב את המשוואה כ-y = f (x B) - f (x A) x B - x A x - x A + f (x A) או
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .
הסקאנט מחלק את הגרף חזותית ל-3 חלקים: משמאל לנקודה A, מ-A ל-B, מימין ל-B. האיור שלהלן מראה שיש שלושה סקנטים שנחשבים זהים, כלומר, הם להגדיר באמצעות משוואה דומה.

מעצם הגדרתו, ברור שהקו והסילוק שלו חופפים במקרה זה.
סקאנט יכול לחתוך את הגרף של פונקציה נתונה מספר פעמים. אם יש משוואה בצורת y \u003d 0 עבור הסקאנט, אז מספר נקודות החיתוך עם הסינוסואיד הוא אינסופי.
הגדרה 5
טנגנט לגרף של הפונקציה f (x) בנקודה x 0 ; f (x 0) נקרא קו ישר העובר דרך נקודה נתונה x 0; f (x 0), עם נוכחות של קטע שיש לו ערכי x רבים הקרובים ל-x 0 .
דוגמה 1
בואו נסתכל מקרוב על הדוגמה שלהלן. אז ניתן לראות שהישר שניתן על ידי הפונקציה y = x + 1 נחשב למשיק ל- y = 2 x בנקודה עם הקואורדינטות (1 ; 2) . למען הבהירות, יש צורך לשקול גרפים עם ערכים קרובים ל- (1; 2). הפונקציה y = 2 x מסומנת בשחור, הקו הכחול הוא המשיק, הנקודה האדומה היא נקודת החיתוך.

ברור, y \u003d 2 x מתמזג עם הקו y \u003d x + 1.
כדי לקבוע את המשיק, יש לשקול את התנהגות המשיק A B כאשר נקודה B מתקרבת לנקודה A באופן אינסופי. לשם הבהירות, אנו מציגים איור.

הגזרה A B, המצוינת בקו הכחול, נוטה למיקום המשיק עצמו, וזווית הנטייה של הגזרה α תתחיל להתקרב לזווית הנטייה של המשיק עצמו α x.
הגדרה 6
המשיק לגרף של הפונקציה y \u003d f (x) בנקודה A הוא המיקום המגביל של הססקנט A B ב-B הנוטה ל-A, כלומר B → A.
כעת נעבור לבחינה של המשמעות הגיאומטרית של הנגזרת של פונקציה בנקודה.
נעבור לשיקול הקטע A B עבור הפונקציה f (x), כאשר A ו-B עם קואורדינטות x 0, f (x 0) ו-x 0 + ∆ x, f (x 0 + ∆ x), ו- ∆ x מסומן כתוספת של הארגומנט. כעת הפונקציה תקבל את הצורה ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . לשם הבהירות, בואו ניקח תמונה כדוגמה.

חשבו על המשולש הישר-זוויתי המתקבל A B C. אנו משתמשים בהגדרת המשיק לפתרון, כלומר נקבל את היחס ∆ y ∆ x = t g α . מהגדרת משיק נובע כי lim ∆ x → 0 ∆ y ∆ x = t g α x . לפי כלל הנגזרת בנקודה, יש לנו שהנגזרת f (x) בנקודה x 0 נקראת הגבול של היחס בין התוספת של הפונקציה לתוספת של הארגומנט, כאשר ∆ x → 0, אז מסומן כ-f (x 0) = lim ∆ x → 0 ∆ y ∆ x .
מכאן נובע ש- f "(x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, כאשר k x מסומן כשיפוע המשיק.
כלומר, נקבל ש-f' (x) יכול להתקיים בנקודה x 0 וכן המשיק לגרף הנתון של הפונקציה בנקודת המגע השווה ל-x 0 , f 0 (x 0) , כאשר הערך של שיפוע המשיק בנקודה שווה לנגזרת בנקודה x 0 . אז נקבל ש-k x = f "(x 0) .
המשמעות הגיאומטרית של הנגזרת של פונקציה בנקודה היא שהמושג של קיומו של משיק לגרף באותה נקודה נתון.
כדי לכתוב את המשוואה של כל ישר במישור, יש צורך בשיפוע עם הנקודה שדרכה הוא עובר. ייעודו נלקח כ- x 0 בצומת.
משוואת המשיק לגרף של הפונקציה y \u003d f (x) בנקודה x 0, f 0 (x 0) מקבלת את הצורה y \u003d f "(x 0) x - x 0 + f (x 0).
זה אומר שהערך הסופי של הנגזרת f "(x 0) יכול לקבוע את מיקום המשיק, כלומר אנכית בתנאי lim x → x 0 + 0 f" (x) = ∞ ו-lim x → x 0 - 0 f "(x ) = ∞ או היעדרות בכלל בתנאי lim x → x 0 + 0 f "(x) ≠ lim x → x 0 - 0 f "(x) .
מיקומו של המשיק תלוי בערך השיפוע שלו k x \u003d f "(x 0). כאשר הוא מקביל לציר x, אנו מקבלים את זה k k \u003d 0, כאשר הוא מקביל בערך y - k x \u003d ∞, ואת ה צורת משוואת המשיק x \u003d x 0 גדלה עם k x > 0 , יורדת ככל k x< 0 .
דוגמה 2
הרכיב את משוואת המשיק לגרף של הפונקציה y \u003d e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 בנקודה עם קואורדינטות (1; 3) עם הגדרת הזווית של יֵצֶר.
פִּתָרוֹן
בהנחה, יש לנו שהפונקציה מוגדרת עבור כל המספרים הממשיים. נקבל שהנקודה עם הקואורדינטות המצוינות בתנאי (1 ; 3) היא נקודת המגע, ואז x 0 = - 1 , f (x 0) = - 3 .
יש צורך למצוא את הנגזרת בנקודה עם ערך -1. אנחנו מקבלים את זה
y "= e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3" = = e x + 1 "+ x 3 3" - 6 - 3 3 x "- 17 - 3 3" = e x + 1 + x 2 - 6 - 3 3 y "(x 0) = y" (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3
הערך של f ' (x) בנקודת המגע הוא השיפוע של הטנגנס, השווה לטנגנס של השיפוע.
ואז k x = t g α x = y "(x 0) = 3 3
מכאן נובע ש- α x = a r c t g 3 3 = π 6
תשובה:משוואת המשיק לובשת את הצורה
y \u003d f "(x 0) x - x 0 + f (x 0) y \u003d 3 3 (x + 1) - 3 y \u003d 3 3 x - 9 - 3 3
לשם הבהירות, אנו נותנים דוגמה באיור גרפי.
צבע שחור משמש לגרף של הפונקציה המקורית, צבע כחול הוא התמונה המשיקת, נקודה אדומה היא נקודת המגע. האיור מימין מציג תצוגה מוגדלת.

דוגמה 3
גלה את קיומו של משיק לגרף של פונקציה נתונה
y = 3 x - 1 5 + 1 בנקודה עם קואורדינטות (1 ; 1) . כתבו משוואה וקבעו את זווית הנטייה.
פִּתָרוֹן
לפי ההנחה, יש לנו שהתחום של הפונקציה הנתונה הוא קבוצת כל המספרים הממשיים.
בואו נעבור למציאת הנגזרת
y "= 3 x - 1 5 + 1" = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5
אם x 0 = 1, אז f ' (x) אינו מוגדר, אבל הגבולות נכתבים כ-lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 1 + 0 = + ∞ ו-lim x → 1 - 0 3 5 1 (x - 1) 4 5 = 3 5 1 (- 0) 4 5 = 3 5 1 + 0 = + ∞ , כלומר קיום משיק אנכי ב נקודה (1; 1).
תשובה:המשוואה תקבל את הצורה x \u003d 1, כאשר זווית הנטייה תהיה שווה ל-π 2.
בוא נרשום את זה לבהירות.

דוגמה 4
מצא את הנקודות של גרף הפונקציות y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 , כאשר
- המשיק אינו קיים;
- המשיק מקביל ל-x;
- המשיק מקביל לישר y = 8 5 x + 4 .
פִּתָרוֹן
יש לשים לב לתחום ההגדרה. בהנחה, יש לנו שהפונקציה מוגדרת על קבוצת כל המספרים הממשיים. הרחב את המודול ופתור את המערכת במרווחים x ∈ - ∞ ; 2 ו-[-2; +∞). אנחנו מקבלים את זה
y = - 1 15 x 3 + 18 x 2 + 105 x + 176, x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; +∞)
יש להבדיל בין הפונקציה. יש לנו את זה
y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 ", x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 " , x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; +∞)
כאשר x = - 2, אז הנגזרת לא קיימת מכיוון שהגבולות החד-צדדיים אינם שווים בנקודה זו:
lim x → - 2 - 0 y "(x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y "(x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3
אנו מחשבים את הערך של הפונקציה בנקודה x \u003d - 2, שם אנו מקבלים את זה
- y (- 2) \u003d 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 \u003d - 2, כלומר, המשיק ב- נקודה (- 2; - 2) לא תתקיים.
- המשיק מקביל ל-x כאשר השיפוע הוא אפס. ואז k x \u003d t g α x \u003d f "(x 0). כלומר, יש צורך למצוא את הערכים של x כזה כאשר הנגזרת של הפונקציה הופכת אותו לאפס. כלומר, הערכים \u200b\u200bof f ' (x) ויהוו נקודות מגע, שבהן המשיק מקביל בערך x .
כאשר x ∈ - ∞ ; - 2 , ואז - 1 5 (x 2 + 12 x + 35) = 0 , ועבור x ∈ (- 2 ; + ∞) נקבל 1 5 (x 2 - 4 x + 3) = 0 .
1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞
אנו מחשבים את הערכים המתאימים של הפונקציה
y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3
מכאן - 5; 8 5 , - 4 ; 4 3 , 1 ; 85, 3; 4 3 נחשבות לנקודות הרצויות בגרף הפונקציה.
שקול ייצוג גרפי של הפתרון.

הקו השחור הוא הגרף של הפונקציה, הנקודות האדומות הן נקודות המגע.
- כאשר הקווים מקבילים, המדרונות שווים. לאחר מכן יש צורך לחפש את נקודות הגרף של הפונקציה, כאשר השיפוע יהיה שווה לערך 8 5 . כדי לעשות זאת, עליך לפתור משוואה בצורה y "(x) = 8 5. ואז, אם x ∈ - ∞; - 2, נקבל את זה - 1 5 (x 2 + 12 x + 35) = 8 5, ואם x ∈ ( - 2 ; + ∞), אז 1 5 (x 2 - 4 x + 3) = 8 5 .
למשוואה הראשונה אין שורשים כי המבחין קטן מאפס. בוא נרשום את זה
1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0
למשוואה אחרת יש שני שורשים אמיתיים, אם כן
1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞
נעבור למציאת ערכי הפונקציה. אנחנו מקבלים את זה
y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3
נקודות עם ערכים - 1; 4 15 , 5 ; 8 3 הן הנקודות שבהן המשיקים מקבילים לישר y = 8 5 x + 4 .
תשובה:קו שחור - גרף של הפונקציה, קו אדום - גרף y \u003d 8 5 x + 4, קו כחול - משיקים בנקודות - 1; 4 15 , 5 ; 8 3 .

קיומו של מספר אינסופי של משיקים עבור פונקציות נתונות אפשרי.
דוגמה 5
כתוב את המשוואות של כל המשיקים הזמינים של הפונקציה y = 3 cos 3 2 x - π 4 - 1 3 , המאונכים לישר y = - 2 x + 1 2 .
פִּתָרוֹן
כדי לשרטט את משוואת המשיק, יש צורך למצוא את המקדם ואת הקואורדינטות של נקודת המגע, בהתבסס על מצב הניצב של הקווים. ההגדרה נשמעת כך: מכפלת המדרונות המאונכים לקווים הישרים שווה ל- 1, כלומר נכתב כ- k x · k ⊥ = - 1. מהתנאי שיש לנו שהשיפוע מאונך לישר ושווה ל- k ⊥ = - 2, ואז k x = - 1 k ⊥ = - 1 - 2 = 1 2 .
כעת עלינו למצוא את הקואורדינטות של נקודות המגע. אתה צריך למצוא את x, ואחריו הערך שלו עבור פונקציה נתונה. שימו לב כי מהמשמעות הגיאומטרית של הנגזרת בנקודה
x 0 נקבל את זה k x \u003d y "(x 0) . מתוך שוויון זה, אנו מוצאים את ערכי x עבור נקודות המגע.
אנחנו מקבלים את זה
y "(x 0) = 3 cos 3 2 x 0 - π 4 - 1 3" = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 \u003d - 9 2 sin 3 2 x 0 - π 4 ⇒ k x \u003d y "(x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 \u003d 1 2 χ sin 3 2 x 0 - 4 = - 1 9
זֶה משוואה טריגונומטריתישמש לחישוב האורדינאטות של נקודות המגע.
3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk או 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk
3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk או 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk
x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk או x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Z הוא קבוצת המספרים השלמים.
נמצאו x נקודות מגע. כעת עליך לעבור לחיפוש ערכי y:
y 0 = 3 cos 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 או y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - - 1 9 2 - 1 3 או y 0 = 3 - 1 - - 1 9 2 - 1 3
y 0 = 4 5 - 1 3 או y 0 = - 4 5 + 1 3
מכאן נקבל ש-2 3 π 4 - a r c sin 1 9 + 2 πk; 4 5 - 1 3, 2 3 5 π 4 + a r c sin 1 9 + 2 πk; - 4 5 + 1 3 הן נקודות מגע.
תשובה:המשוואות הדרושות ייכתבו כ
y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3, y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z
עבור ייצוג חזותי, שקול את הפונקציה ואת המשיק על קו הקואורדינטות.
האיור מראה שמיקום הפונקציה הוא על המרווח [-10; 10 ] , כאשר הקו השחור הוא גרף הפונקציה, הקווים הכחולים הם משיקים המאונכים לישר הנתון בצורה y = - 2 x + 1 2 . נקודות אדומות הן נקודות מגע.

המשוואות הקנוניות של עקומות מהסדר השני אינן פונקציות חד-ערך. משוואות טנגנטיות עבורם מורכבות לפי סכמות ידועות.
טנג'נט למעגל
לקבוע מעגל במרכזו בנקודה x c e n t e r; y c e n t e r ורדיוס R, נעשה שימוש בנוסחה x - x c e n t e r 2 + y - y c e n t e r 2 = R 2.
ניתן לכתוב שוויון זה כאיחוד של שתי פונקציות:
y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r
הפונקציה הראשונה נמצאת בחלק העליון והשנייה בתחתית, כפי שמוצג באיור.

לשרטט משוואת מעגל בנקודה x 0; y 0, הממוקם בחצי המעגל העליון או התחתון, אתה צריך למצוא את המשוואה של גרף הפונקציה של הצורה y \u003d R 2 - x - x c e n t e r 2 + y c e n t e r או y \u003d - R 2 - x - 2 e + y c e n t e r בנקודה שצוינה.
כאשר בנקודות x c e n t e r; y c e n t e r + R ו-x c e n t e r; ניתן לתת משיקים y c e n t e r - R על ידי המשוואות y = y c e n t e r + R ו- y = y c e n t e r - R, ובנקודות x c e n t e r + R; y c e n t e r and
x c e n t e r - R; y c e n t e r יהיה מקביל לגבי y, ואז נקבל משוואות בצורה x = x c e n t e r + R ו-x = x c e n t e r - R .

טנג'נט לאליפס
כאשר האליפסה מרוכזת ב-x c e n t e r; y c e n t e r עם צירים למחצה a ו- b , אז ניתן לתת אותו באמצעות המשוואה x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 .
ניתן לציין אליפסה ומעגל על ידי שילוב של שתי פונקציות, כלומר חצי אליפסה עליונה והתחתונה. ואז נקבל את זה
y = b a a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a a 2 - (x - x c e n t e r) 2 + y c e n t e r

אם המשיקים ממוקמים בקודקודי האליפסה, אז הם מקבילים בערך x או בערך y. לבהירות, שקול את האיור שלהלן.

דוגמה 6
כתוב את משוואת המשיק לאליפסה x - 3 2 4 + y - 5 2 25 = 1 בנקודות עם ערכי x שווים ל- x = 2 .
פִּתָרוֹן
יש צורך למצוא נקודות מגע המתאימות לערך x = 2. אנו מבצעים החלפה במשוואה הקיימת של האליפסה ומשיגים זאת
x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5
ואז 2; 5 3 2 + 5 ו-2; - 5 3 2 + 5 הן נקודות המשיק השייכות לחצי אליפסה העליונה והתחתונה.
נעבור למציאת ופתירת משוואת אליפסה ביחס ל-y. אנחנו מקבלים את זה
x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2
ברור שהחצי אליפסה העליונה מצוינת באמצעות פונקציה של הצורה y = 5 + 5 2 4 - x - 3 2, והתחתון y = 5 - 5 2 4 - x - 3 2 .
אנו מיישמים את האלגוריתם הסטנדרטי על מנת לנסח את משוואת המשיק לגרף של פונקציה בנקודה. אנו כותבים כי המשוואה עבור המשיק הראשון בנקודה 2; 5 3 2 + 5 ייראה
y "= 5 + 5 2 4 - x - 3 2" = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y "(x 0) = y" (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5
אנו מקבלים את המשוואה של המשיק השני עם הערך בנקודה
2; - 5 3 2 + 5 הופכים
y "= 5 - 5 2 4 - (x - 3) 2" = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y "(x 0) = y" (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5
מבחינה גרפית, משיקים מסומנים כדלקמן:

טגנט להפרעה
כאשר להיפרבולה יש מרכז בנקודה x c e n t e r; y c e n t e r וקודקודים x c e n t e r + α ; y c e n t e r ו-x c e n t e r - α ; y c e n t e r , אי השוויון x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 ניתן אם עם קודקודים x c e n t e r ; y c e n t e r + b ו-x c e n t e r; y c e n t e r-b ניתן אז על ידי אי השוויון x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

היפרבולה יכולה להיות מיוצגת כשתי פונקציות משולבות של הצורה
y = b a (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a (x - x c e n t e r) 2 - a 2 + y c e n t e r or y = b a (x - x c e r + b a (x - x c e r + e) ) 2 + a 2 + y c e n t e r

במקרה הראשון, יש לנו שהמשיקים מקבילים ל-y, ובמקרה השני, הם מקבילים ל-x.
מכאן נובע שכדי למצוא את משוואת המשיק להיפרבולה, יש צורך לברר לאיזו פונקציה שייכת נקודת המשיק. כדי לקבוע זאת, יש צורך לבצע החלפה במשוואות ולבדוק את זהותן.
דוגמה 7
כתוב את משוואת המשיק להיפרבולה x - 3 2 4 - y + 3 2 9 = 1 בנקודה 7; - 3 3 - 3 .
פִּתָרוֹן
יש צורך להפוך את הרשומה של הפתרון של מציאת ההיפרבולה באמצעות 2 פונקציות. אנחנו מקבלים את זה
x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 או y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3
יש צורך לברר לאיזו פונקציה שייכת הנקודה הנתונה עם קואורדינטות 7; - 3 3 - 3 .
ברור, כדי לבדוק את הפונקציה הראשונה, אתה צריך y (7) = 3 2 (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, אז הנקודה לא שייכת לגרף, שכן השוויון אינו מרוצה.
עבור הפונקציה השנייה, יש לנו ש-y (7) = - 3 2 (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 , כלומר הנקודה שייכת לגרף הנתון. מכאן אתה אמור למצוא את מקדם השיפוע.
אנחנו מקבלים את זה
y "= - 3 2 (x - 3) 2 - 4 - 3" = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y "(x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3
תשובה:ניתן לייצג את משוואת המשיק כ
y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3
זה מוצג בצורה חזותית כדלקמן:

טנג'נט לפרבולה
כדי להרכיב את משוואת המשיק לפרבולה y \u003d a x 2 + b x + c בנקודה x 0, y (x 0), עליך להשתמש באלגוריתם הסטנדרטי, ואז המשוואה תקבל את הצורה y \u003d y " (x 0) x - x 0 + y ( x 0) משיק כזה בקודקוד מקביל ל-x.
יש להגדיר את הפרבולה x = a y 2 + b y + c כאיחוד של שתי פונקציות. לכן, עלינו לפתור את המשוואה עבור y. אנחנו מקבלים את זה
x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a
בוא נרשום את זה כ:

כדי לגלות אם נקודה x 0 , y (x 0) שייכת לפונקציה, פעל בעדינות לפי האלגוריתם הסטנדרטי. משיק כזה יהיה מקביל ל-y ביחס לפרבולה.
דוגמה 8
כתוב את משוואת המשיק לגרף x - 2 y 2 - 5 y + 3 כאשר יש לנו שיפוע משיק של 150 מעלות.
פִּתָרוֹן
אנחנו מתחילים את הפתרון על ידי ייצוג הפרבולה כשתי פונקציות. אנחנו מקבלים את זה
2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 (- 2) (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4
ערך השיפוע שווה לערך הנגזרת בנקודה x 0 של פונקציה זו ושווה לטנגנס של השיפוע.
אנחנו מקבלים:
k x \u003d y "(x 0) \u003d t g α x \u003d t g 150 ° \u003d - 1 3
מכאן אנו קובעים את הערך של x עבור נקודות המגע.
הפונקציה הראשונה תיכתב בשם
y "= 5 + 49 - 8 x - 4" = 1 49 - 8 x ⇒ y "(x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3
ברור שאין שורשים אמיתיים, שכן קיבלנו ערך שלילי. אנו מסיקים שאין משיק עם זווית של 150 מעלות עבור פונקציה כזו.
הפונקציה השנייה תיכתב בשם
y "= 5 - 49 - 8 x - 4" = - 1 49 - 8 x ⇒ y "(x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4
יש לנו שנקודות המגע - 23 4; - 5 + 3 4 .
תשובה:משוואת המשיק לובשת את הצורה
y = - 1 3 x - 23 4 + - 5 + 3 4
בוא נרשום את זה בצורה כזו:
אם אתה מבחין בטעות בטקסט, אנא סמן אותה והקש Ctrl+Enter
עַל השלב הנוכחיפיתוח החינוך כאחת המשימות העיקריות שלו היא גיבוש אישיות בעלת חשיבה יצירתית. ניתן לפתח את יכולת היצירתיות של התלמידים רק אם הם מעורבים באופן שיטתי ביסודות פעילויות המחקר. בסיס לסטודנטים ליישם את שלהם כוחות יצירתיים, יכולות וכישרונות נוצרים ידע ומיומנויות מן המניין. בהקשר זה ישנה חשיבות לא קטנה לבעיה של גיבוש מערכת של ידע ומיומנויות בסיסיות לכל נושא בקורס המתמטיקה בבית הספר. יחד עם זאת, כישורים מן המניין צריכים להיות מטרה דידקטיתלא משימות בודדות, אלא מערכת מחושבת בקפידה שלהן. במובן הרחב, מערכת מובנת כמערכת של אלמנטים המתקשרים זה בזה, שיש להם שלמות ומבנה יציב.
שקול מתודולוגיה ללמד תלמידים כיצד לשרטט משוואה של משיק לגרף פונקציה. בעצם, כל המטלות למציאת משוואת המשיק מצטמצמות לצורך לבחור מתוך קבוצת הקווים (שלמה, משפחה) את אלו מהן העונות על דרישה מסוימת - הן משיקות לגרף של פונקציה מסוימת. במקרה זה, ניתן לציין את קבוצת השורות שמהן מתבצעת הבחירה בשתי דרכים:
א) נקודה השוכבת על מישור xOy (עיפרון מרכזי של קווים);
ב) מקדם זוויתי (צרור מקביל של קווים).
בהקשר זה, כאשר למדנו את הנושא "משגע לגרף של פונקציה" על מנת לבודד את מרכיבי המערכת, זיהינו שני סוגים של משימות:
1) משימות על משיק, נְקוּדָהשדרכו הוא עובר;
2) משימות על משיק שניתן על ידי השיפוע שלו.
לימוד פתרון בעיות על טנגנס בוצע באמצעות האלגוריתם שהציע א.ג. מורדקוביץ'. ההבדל הבסיסי שלו מהידועים כבר הוא שהאבשיסה של נקודת המשיק מסומנת באות a (במקום x0), שבקשר אליה משוואת המשיק לובשת את הצורה
y \u003d f (a) + f "(a) (x - a)
(השווה עם y \u003d f (x 0) + f "(x 0) (x - x 0)). טכניקה מתודולוגית זו, לדעתנו, מאפשרת לתלמידים להבין במהירות ובקלות היכן כתובות הקואורדינטות של הנקודה הנוכחית במשוואת המשיק הכללית, והיכן נקודות המגע.
אלגוריתם להרכבת משוואת המשיק לגרף של הפונקציה y = f(x)
1. סמן באות a את האבשיסה של נקודת המגע.
2. מצא את f(a).
3. מצא את f "(x) ו-f "(a).
4. החלף את המספרים שנמצאו a, f (a), f "(a) לתוך משוואה כלליתמשיק y \u003d f (a) \u003d f "(a) (x - a).
ניתן להרכיב אלגוריתם זה על בסיס בחירה עצמאית של פעולות של התלמידים ורצף ביצוען.
התרגול הראה שהפתרון העקבי של כל אחת ממשימות המפתח באמצעות האלגוריתם מאפשר לך ליצור את היכולת לכתוב את משוואת המשיק לגרף של הפונקציה בשלבים, ושלבי האלגוריתם משמשים כנקודות חזקות לפעולות . גישה זו תואמת את התיאוריה של היווצרות הדרגתית של פעולות נפשיות שפותחה על ידי P.Ya. גלפרין ונ.פ. טאליזין.
בסוג המשימות הראשון זוהו שתי משימות מפתח:
- המשיק עובר דרך נקודה השוכבת על העקומה (בעיה 1);
- המשיק עובר דרך נקודה שאינה מונחת על העקומה (בעיה 2).
משימה 1. השוו את המשיק לגרף של הפונקציה ![]() בנקודה M(3; – 2).
בנקודה M(3; – 2).
פִּתָרוֹן. הנקודה M(3; – 2) היא נקודת המגע, שכן
1. a = 3 - אבשיסה של נקודת המגע.
2. f(3) = – 2.
3. f "(x) \u003d x 2 - 4, f "(3) \u003d 5.
y \u003d - 2 + 5 (x - 3), y \u003d 5x - 17 היא משוואת המשיק.
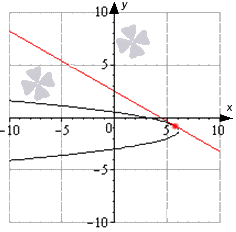
משימה 2. כתוב את המשוואות של כל המשיקים לגרף של הפונקציה y = - x 2 - 4x + 2, עוברים דרך הנקודה M(- 3; 6).
 פִּתָרוֹן. הנקודה M(– 3; 6) אינה נקודת משיק, שכן f(– 3) 6 (איור 2).
פִּתָרוֹן. הנקודה M(– 3; 6) אינה נקודת משיק, שכן f(– 3) 6 (איור 2).
2. f(a) = – a 2 – 4a + 2.
3. f "(x) \u003d - 2x - 4, f "(a) \u003d - 2a - 4.
4. y \u003d - a 2 - 4a + 2 - 2 (a + 2) (x - a) - משוואת משיק.
הטנגנס עובר דרך הנקודה M(– 3; 6), לכן, הקואורדינטות שלו עומדות במשוואת המשיק.
6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0 ^ a 1 = - 4, a 2 = - 2.
אם a = – 4, אז משוואת המשיק היא y = 4x + 18.
אם \u003d - 2, אז למשוואת המשיק יש את הצורה y \u003d 6.
בסוג השני, משימות המפתח יהיו הבאות:
- המשיק מקביל לקו ישר כלשהו (בעיה 3);
- המשיק עובר בזווית כלשהי לישר הנתון (בעיה 4).
משימה 3. כתוב את המשוואות של כל המשיקים לגרף של הפונקציה y \u003d x 3 - 3x 2 + 3, במקביל לישר y \u003d 9x + 1.
1. א - אבשיסה של נקודת המגע.
2. f(a) = a 3 - 3a 2 + 3.
3. f "(x) \u003d 3x 2 - 6x, f "(a) \u003d 3a 2 - 6a.
 אבל, מצד שני, f "(א) \u003d 9 (מצב מקביליות). אז, אנחנו צריכים לפתור את המשוואה 3a 2 - 6a \u003d 9. השורשים שלו a \u003d - 1, a \u003d 3 (איור .3).
אבל, מצד שני, f "(א) \u003d 9 (מצב מקביליות). אז, אנחנו צריכים לפתור את המשוואה 3a 2 - 6a \u003d 9. השורשים שלו a \u003d - 1, a \u003d 3 (איור .3).
4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9(x + 1);
y = 9x + 8 היא משוואת המשיק;
1) a = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) y = 3 + 9(x - 3);
y = 9x – 24 היא משוואת המשיק.
 משימה 4. כתוב את משוואת המשיק לגרף של הפונקציה y = 0.5x 2 - 3x + 1, עובר בזווית של 45° לישר y = 0 (איור 4).
משימה 4. כתוב את משוואת המשיק לגרף של הפונקציה y = 0.5x 2 - 3x + 1, עובר בזווית של 45° לישר y = 0 (איור 4).
פִּתָרוֹן. מהתנאי f "(a) \u003d tg 45 ° אנו מוצאים את a: a - 3 \u003d 1 ^ a \u003d 4.
1. a = 4 - אבשיסה של נקודת המגע.
2. f(4) = 8 - 12 + 1 = - 3.
3. f "(4) \u003d 4 - 3 \u003d 1.
4. y \u003d - 3 + 1 (x - 4).
y \u003d x - 7 - משוואת המשיק.
קל להראות שהפתרון של כל בעיה אחרת מצטמצם לפתרון של בעיה מרכזית אחת או כמה. שקול את שתי הבעיות הבאות כדוגמה.
 1. כתוב את משוואות המשיקים לפרבולה y = 2x 2 - 5x - 2, אם המשיקים נחתכים בזווית ישרה ואחד מהם נוגע בפרבולה בנקודה עם האבשיסה 3 (איור 5).
1. כתוב את משוואות המשיקים לפרבולה y = 2x 2 - 5x - 2, אם המשיקים נחתכים בזווית ישרה ואחד מהם נוגע בפרבולה בנקודה עם האבשיסה 3 (איור 5).
פִּתָרוֹן. מכיוון שהאבססיס של נקודת המגע ניתנת, החלק הראשון של הפתרון מצטמצם לבעיית המפתח 1.
1. a = 3 - אבשסיס של נקודת המגע של אחד הצדדים זווית נכונה.
2. f(3) = 1.
3. f "(x) \u003d 4x - 5, f "(3) \u003d 7.
4. y \u003d 1 + 7 (x - 3), y \u003d 7x - 20 - משוואת המשיק הראשון.
תן ל-a להיות השיפוע של המשיק הראשון. מכיוון שהמשיקים מאונכים, אז היא זווית הנטייה של המשיק השני. מהמשוואה y = 7x – 20 של המשיק הראשון יש לנו tg a = 7. מצא
![]()
זה אומר שהשיפוע של המשיק השני הוא .
הפתרון הנוסף מצטמצם למשימת המפתח 3.
תנו ל-B(c; f(c)) להיות נקודת המשיק של הישר השני, אם כן
1. - אבשיסה של נקודת המגע השנייה.
2. ![]()
3. ![]()
4. ![]()
![]() היא משוואת המשיק השני.
היא משוואת המשיק השני.
הערה. ניתן למצוא קל יותר את המקדם הזוויתי של המשיק אם התלמידים יודעים את היחס בין המקדמים של ישרים מאונכים k 1 k 2 = - 1.
2. כתוב את המשוואות של כל המשיקים הנפוצים לגרפי פונקציה
 פִּתָרוֹן. המשימה מצטמצמת למציאת האבססיס של נקודות המגע של המשיקים המשותפים, כלומר לפתרון בעיית המפתח 1 בצורה כללית, הרכבת מערכת משוואות ואז פתרונה (איור 6).
פִּתָרוֹן. המשימה מצטמצמת למציאת האבססיס של נקודות המגע של המשיקים המשותפים, כלומר לפתרון בעיית המפתח 1 בצורה כללית, הרכבת מערכת משוואות ואז פתרונה (איור 6).
1. תן ל-a להיות האבססיס של נקודת המגע המונחת על גרף הפונקציה y = x 2 + x + 1.
2. f(a) = a 2 + a + 1.
3. f "(a) = 2a + 1.
4. y \u003d a 2 + a + 1 + (2a + 1) (x - a) \u003d (2a + 1) x + 1 - a 2.
1. תנו ל-c להיות האבססיס של נקודת המשיק המונחת על גרף הפונקציה ![]()
2. ![]()
3. f "(ג) = ג.
4.
מכיוון שהמשיקים שכיחים, אז

אז y = x + 1 ו- y = - 3x - 3 הם משיקים נפוצים.
המטרה העיקרית של המשימות הנחשבות היא להכין את התלמידים להכרה עצמית של סוג משימת המפתח כאשר הם פותרים יותר משימות מאתגרותהדורשים מיומנויות מחקר מסוימות (היכולת לנתח, להשוות, להכליל, להעלות השערה וכו'). משימות כאלה כוללות כל משימה שבה משימת המפתח כלולה כרכיב. הבה נבחן כדוגמה את הבעיה (הפוכה לבעיה 1) של מציאת פונקציה ממשפחת המשיקים שלה.
3. עבור אילו b ו-c הם הקווים y \u003d x ו-y \u003d - 2x משיקים לגרף של הפונקציה y \u003d x 2 + bx + c?
תן t להיות האבססיס של נקודת המגע של הישר y = x עם הפרבולה y = x 2 + bx + c; p היא האבססיס של נקודת המגע של הישר y = - 2x עם הפרבולה y = x 2 + bx + c. אז משוואת המשיק y = x תקבל את הצורה y = (2t + b)x + c - t 2 , ומשוואת המשיק y = - 2x תקבל את הצורה y = (2p + b)x + c - p 2 .
לחבר ולפתור מערכת משוואות

תשובה: ![]()
הטנגנט הוא קו ישר , הנוגע בגרף של הפונקציה בנקודה אחת וכל הנקודות שלה נמצאות במרחק הקטן ביותר מגרף הפונקציה. לכן, המשיק עובר משיק לגרף הפונקציה בזווית מסוימת ומספר משיקים לא יכולים לעבור דרך נקודת המשיק בזוויות שונות. משוואות המשיק ומשוואות הנורמלי לגרף הפונקציה מורכבות באמצעות הנגזרת.
משוואת המשיק נגזרת ממשוואת הישר .
נגזר את משוואת הטנגנס, ולאחר מכן את משוואת הנורמל לגרף הפונקציה.
y = kx + ב .
בו ק- מקדם זוויתי.
מכאן נקבל את הערך הבא:
y - y 0 = ק(איקס - איקס 0 ) .
ערך נגזר ו "(איקס 0 ) פונקציות y = ו(איקס) בנקודה איקס0 שווה למדרון ק=tg φ משיק לגרף של פונקציה המצוירת דרך נקודה M0 (איקס 0 , y 0 ) , איפה y0 = ו(איקס 0 ) . זה מה משמעות גיאומטרית של הנגזרת .
כך נוכל להחליף קעַל ו "(איקס 0 ) וקבל את הדברים הבאים משוואת המשיק לגרף הפונקציה :
y - y 0 = ו "(איקס 0 )(איקס - איקס 0 ) .
במשימות להרכבת משוואת משיק לגרף של פונקציה (ותכף נעבור אליהן), נדרש להביא את המשוואה המתקבלת מהנוסחה הנ"ל ל משוואה כללית של קו ישר. לשם כך, עליך להעביר את כל האותיות והמספרים אל צד שמאלמשוואה, ולהשאיר אפס בצד ימין.
עכשיו לגבי המשוואה הרגילה. נוֹרמָלִי הוא ישר העובר דרך נקודת המשיק לגרף הפונקציה בניצב למשיק. משוואה רגילה :
(איקס - איקס 0 ) + ו "(איקס 0 )(y - y 0 ) = 0
כדי לחמם את הדוגמה הראשונה, אתה מתבקש לפתור אותה בעצמך, ולאחר מכן להסתכל על הפתרון. יש כל סיבה לקוות שהמשימה הזו לא תהיה "מקלחת קרה" עבור קוראינו.
דוגמה 0.חבר את משוואת המשיק ומשוואת הנורמלי לגרף הפונקציה בנקודה M (1, 1) .
דוגמה 1חבר את משוואת הטנגנס ואת משוואת הנורמלי לגרף הפונקציה ![]() אם האבשיסה של נקודת המגע היא .
אם האבשיסה של נקודת המגע היא .
בוא נמצא את הנגזרת של הפונקציה:
כעת יש לנו את כל מה שצריך להחליף לערך שניתן בהתייחסות התיאורטית כדי לקבל את משוואת המשיק. אנחנו מקבלים
![]()
בדוגמה זו, התמזל מזלנו: השיפוע התברר כשווה לאפס, אז הבא את המשוואה בנפרד ל השקפה כלליתלא היה צריך. כעת נוכל לכתוב את המשוואה הרגילה:
![]()
באיור למטה: גרף של פונקציית צבע בורדו, משיק צבע ירוק, הרגיל הוא כתום.

גם הדוגמה הבאה לא מסובכת: הפונקציה, כמו בקודמתה, היא גם פולינום, אבל מקדם השיפוע לא יהיה שווה לאפס, ולכן יתווסף עוד שלב - הבאת המשוואה לצורה כללית.
דוגמה 2
פִּתָרוֹן. בוא נמצא את האורדינאטה של נקודת המגע:
בוא נמצא את הנגזרת של הפונקציה:
![]() .
.
בואו נמצא את הערך של הנגזרת בנקודת המגע, כלומר, שיפוע המשיק:
נחליף את כל הנתונים שהתקבלו ב"נוסחה הריקה" ונקבל את משוואת המשיק:
![]()
אנו מביאים את המשוואה לצורה כללית (אנו אוספים את כל האותיות והמספרים מלבד אפס בצד שמאל, ומשאירים אפס בצד ימין):
אנו מרכיבים את משוואת הנורמלי:

דוגמה 3חבר את משוואת המשיק ואת משוואת הנורמלי לגרף הפונקציה אם האבשיסה של נקודת המגע היא .
פִּתָרוֹן. בוא נמצא את האורדינאטה של נקודת המגע:
בוא נמצא את הנגזרת של הפונקציה:
![]() .
.
בואו נמצא את הערך של הנגזרת בנקודת המגע, כלומר, שיפוע המשיק:
![]() .
.
נמצא את משוואת המשיק:

לפני שמביאים את המשוואה לצורה כללית, צריך "לשלב" אותה קצת: כפול איבר אחר איבר ב-4. נעשה זאת ונביא את המשוואה לצורה כללית:
אנו מרכיבים את משוואת הנורמלי:

דוגמה 4חבר את משוואת המשיק ואת משוואת הנורמלי לגרף הפונקציה אם האבשיסה של נקודת המגע היא .
פִּתָרוֹן. בוא נמצא את האורדינאטה של נקודת המגע:
![]() .
.
בוא נמצא את הנגזרת של הפונקציה:
בואו נמצא את הערך של הנגזרת בנקודת המגע, כלומר, שיפוע המשיק:
![]() .
.
נקבל את משוואת המשיק:
אנו מביאים את המשוואה לצורה כללית:
אנו מרכיבים את משוואת הנורמלי:
![]()
טעות נפוצה בכתיבת משוואות משיקות ונורמליות היא לא לשים לב שהפונקציה שניתנה בדוגמה מורכבת ולחשב את הנגזרת שלה כנגזרת של פונקציה פשוטה. הדוגמאות הבאות כבר פונקציות מורכבות(השיעור המתאים ייפתח בחלון חדש).
דוגמה 5חבר את משוואת המשיק ואת משוואת הנורמלי לגרף הפונקציה אם האבשיסה של נקודת המגע היא .
פִּתָרוֹן. בוא נמצא את האורדינאטה של נקודת המגע:
תשומת הלב! פונקציה זו מורכבת, שכן הארגומנט של הטנגנס (2 איקס) היא בעצמה פונקציה. לכן, אנו מוצאים את הנגזרת של פונקציה כנגזרת של פונקציה מורכבת.
שלב ראשון
משוואת המשיק לגרף הפונקציה. מדריך מקיף (2019)
אתה כבר יודע מהי נגזרת? אם לא, קרא קודם את השרשור. אז אתה אומר שאתה מכיר את הנגזרת. עכשיו בואו נבדוק. מצא את התוספת של הפונקציה כאשר התוספת של הארגומנט שווה ל. הסתדרת? זה אמור לעבוד. כעת מצא את הנגזרת של הפונקציה בנקודה. תשובה: . קרה? אם אחת מהדוגמאות הללו קשה, אני ממליץ בחום לחזור לנושא וללמוד אותו שוב. אני יודע שהנושא מאוד גדול, אבל חוץ מזה אין טעם ללכת רחוק יותר. שקול את הגרף של פונקציה כלשהי:
בואו נבחר נקודה מסוימת על קו הגרף. תן האבססיס שלה, ואז הסמין שווה. לאחר מכן נבחר נקודה קרובה לנקודה עם אבשיסה; הסידור שלו הוא:

בואו נצייר קו דרך הנקודות הללו. זה נקרא סקאנט (בדיוק כמו בגיאומטריה). הבה נסמן את זווית הנטייה של הקו הישר לציר כ. כמו בטריגונומטריה, זווית זו נמדדת מהכיוון החיובי של ציר ה-x נגד כיוון השעון. אילו ערכים זווית יכולה לקחת? לא משנה איך תטה את הקו הישר הזה, חצי אחד עדיין יישאר למעלה. לכן, הזווית המקסימלית האפשרית היא , והמינימום האפשרי הוא . אומר, . הזווית אינה כלולה, מכיוון שהמיקום של הקו במקרה זה תואם בדיוק, וזה הגיוני יותר לבחור זווית קטנה יותר. קח נקודה באיור כך שהקו הישר יהיה מקביל לציר האבשיסה, ו- סדין:

ניתן לראות מהאיור כי א. ואז היחס בין המרווחים:
(כי הוא מלבני).
בוא נקטין עכשיו. ואז הנקודה תתקרב לנקודה. כאשר הוא הופך לאינפיניטסימלי, היחס הופך להיות שווה לנגזרת של הפונקציה בנקודה. מה יעלה בגורל הסקאנט במקרה זה? הנקודה תהיה קרובה לאין ערוך לנקודה, כך שהם יכולים להיחשב לאותה נקודה. אבל קו ישר שיש לו רק נקודה משותפת אחת עם עקומה הוא לא יותר מאשר מַשִׁיק(במקרה זה, תנאי זה מתקיים רק ב שטח קטן- קרוב לנקודה, אבל זה מספיק). הם אומרים שבמקרה הזה הסקאנט כובש עמדת גבול.
בואו נקרא את זווית הנטייה של הססקנט לציר. ואז מתברר שהנגזרת
זה הנגזרת שווה לטנגנס של שיפוע המשיק לגרף הפונקציה בנקודה נתונה.
מכיוון שהמשיק הוא ישר, נזכיר כעת את המשוואה של ישר:
בשביל מה היחס? עבור השיפוע של קו ישר. זה נקרא כך: מִדרוֹן. מה זה אומר? והעובדה שהוא שווה לטנגנס של הזווית בין הישר לציר! כלומר, זה מה שקורה:
אבל קיבלנו את הכלל הזה על ידי התחשבות בפונקציה הולכת וגדלה. מה קורה אם הפונקציה יורדת? בוא נראה:  עכשיו הפינות בוטות. והתוספת של הפונקציה שלילית. שקול שוב: . בצד השני, . אנחנו מקבלים:, כלומר הכל, כמו בפעם הקודמת. בוא נכוון את הנקודה שוב לנקודה, והסקאנט ייקח את המיקום המגביל, כלומר יהפוך למשיק לגרף של הפונקציה בנקודה. אז בואו ננסח את הכלל הסופי:
עכשיו הפינות בוטות. והתוספת של הפונקציה שלילית. שקול שוב: . בצד השני, . אנחנו מקבלים:, כלומר הכל, כמו בפעם הקודמת. בוא נכוון את הנקודה שוב לנקודה, והסקאנט ייקח את המיקום המגביל, כלומר יהפוך למשיק לגרף של הפונקציה בנקודה. אז בואו ננסח את הכלל הסופי:
הנגזרת של הפונקציה בנקודה נתונה שווה לטנגנס של שיפוע המשיק לגרף הפונקציה בנקודה זו, או (שזה זהה) לשיפוע של משיק זה:
זה מה שזה משמעות גיאומטרית של הנגזרת.אוקיי, כל זה מעניין, אבל למה אנחנו צריכים את זה? כאן דוגמא:
האיור מציג גרף של פונקציה ומשיק לה בנקודה עם אבשיסה. מצא את הערך של הנגזרת של הפונקציה בנקודה. 
פִּתָרוֹן.
כפי שגילינו לאחרונה, ערך הנגזרת בנקודת המגע שווה לשיפוע המשיק, שבתורו שווה לטנגנסזווית הנטייה של המשיק הנתון לציר ה-x:. לכן, כדי למצוא את הערך של הנגזרת, עלינו למצוא את הטנגנס של שיפוע המשיק. באיור, סימנו שתי נקודות המונחות על משיק, שהקואורדינטות שלהן ידועות לנו. אז בואו נשלים את המשולש ישר הזווית העובר בנקודות אלו, ונמצא את הטנגנס של זווית הנטייה של המשיק! 
זווית הנטייה של המשיק לציר היא. בואו נמצא את הטנגנס של זווית זו: . לפיכך, הנגזרת של פונקציה בנקודה שווה ל.
תשובה:. עכשיו נסה את זה בעצמך:

תשובות:

יוֹדֵעַ משמעות גיאומטרית של הנגזרת, אפשר להסביר בפשטות רבה את הכלל שהנגזרת בנקודה של מקסימום או מינימום מקומי שווה לאפס. אכן, המשיק לגרף בנקודות אלו הוא "אופקי", כלומר מקביל לציר ה-x: 
מהי הזווית בין קווים מקבילים? כמובן, אפס! והטנגנס של אפס הוא גם אפס. אז הנגזרת היא אפס:
קרא עוד על כך בנושא "מונוטוניות של פונקציות. נקודות קיצון.
עכשיו בואו נתמקד במשיקים שרירותיים. נניח שיש לנו פונקציה כלשהי, למשל, . שרטטנו את הגרף שלו ואנו רוצים לצייר לו משיק בשלב מסוים. למשל, בשלב מסוים. אנחנו לוקחים סרגל, מצמידים אותו לגרף ומציירים:

מה אנחנו יודעים על הקו הזה? מה הכי חשוב לדעת על קו ישר במישור קואורדינטות? מכיוון שקו ישר הוא תמונה של פונקציה לינארית, יהיה נוח מאוד לדעת את המשוואה שלה. כלומר, המקדמים במשוואה
אבל אנחנו כבר יודעים! זהו השיפוע של הטנגנס, ששווה לנגזרת של הפונקציה באותה נקודה:
בדוגמה שלנו זה יהיה כך:
עכשיו נותר למצוא. זה יותר פשוט מפשוט: אחרי הכל - הערך ב. מבחינה גרפית, זוהי הקואורדינטה של החיתוך של הישר עם ציר ה-y (אחרי הכל, בכל נקודות הציר):

בואו נצייר (כך - מלבני). לאחר מכן (לאותה זווית בין המשיק לציר ה-x). למה הם ושווים? האיור מראה בבירור כי, א. ואז נקבל:
אנו משלבים את כל הנוסחאות שהתקבלו למשוואה של ישר:
עכשיו תחליטו בעצמכם:
- למצוא משוואת משיקיםלפונקציה בנקודה מסוימת.
- המשיק לפרבולה חוצה את הציר בזווית. מצא את המשוואה עבור המשיק הזה.
- הישר מקביל למשיק לגרף הפונקציה. מצא את האבשיסה של נקודת המגע.
- הישר מקביל למשיק לגרף הפונקציה. מצא את האבשיסה של נקודת המגע.
פתרונות ותשובות:

משוואה של טנגנט הפונקציה לגרף. תיאור קצר ונוסחה בסיסית
הנגזרת של הפונקציה בנקודה מסוימת שווה לטנגנס של שיפוע המשיק לגרף הפונקציה בנקודה זו, או שיפוע המשיק הזה:
משוואת המשיק לגרף של פונקציה בנקודה:
אלגוריתם של פעולות למציאת משוואת המשיק:
ובכן, הנושא הסתיים. אם אתה קורא שורות אלה, אתה מאוד מגניב.
כי רק 5% מהאנשים מסוגלים לשלוט במשהו בעצמם. ואם קראתם עד הסוף, אז אתם ב-5%!
עכשיו הדבר הכי חשוב.
הבנת את התיאוריה בנושא זה. ואני חוזר, זה... זה פשוט מעולה! אתה כבר יותר טוב מהרוב המכריע של עמיתיך.
הבעיה היא שאולי זה לא מספיק...
בשביל מה?
על מעבר מוצלח של הבחינה, על קבלה למכון בתקציב והכי חשוב לכל החיים.
אני לא אשכנע אותך בכלום, אני רק אגיד דבר אחד...
אנשים שקיבלו חינוך טוב, מרוויחים הרבה יותר מאלה שלא קיבלו. זו סטטיסטיקה.
אבל זה לא העיקר.
העיקר שהם יותר שמחים (יש מחקרים כאלה). אולי כי הרבה יותר הזדמנויות נפתחות בפניהם והחיים נעשים בהירים יותר? לא יודע...
אבל תחשוב בעצמך...
מה צריך כדי להיות בטוח להיות טוב יותר מאחרים בבחינה ולהיות בסופו של דבר... מאושר יותר?
מלא את היד שלך, פותר בעיות בנושא זה.
בבחינה לא ישאלו אותך תיאוריה.
אתה תצטרך לפתור בעיות בזמן.
ואם לא פתרת אותם (הרבה!), אתה בהחלט תעשה טעות מטופשת איפשהו או פשוט לא תעשה את זה בזמן.
זה כמו בספורט - צריך לחזור על זה הרבה פעמים כדי לנצח בוודאות.
מצא אוסף בכל מקום שתרצה בהכרח עם פתרונות ניתוח מפורט ולהחליט, להחליט, להחליט!
אתה יכול להשתמש במשימות שלנו (לא הכרחי) ואנחנו בהחלט ממליצים עליהן.
כדי לקבל יד בעזרת המשימות שלנו, אתה צריך לעזור להאריך את חיי ספר הלימוד YouClever שאתה קורא כעת.
אֵיך? ישנן שתי אפשרויות:
- בטל את נעילת הגישה לכל המשימות הנסתרות במאמר זה - 299 לשפשף.
- בטל את הנעילה של גישה לכל המשימות הנסתרות בכל 99 המאמרים של המדריך - 999 לשפשף.
כן, יש לנו 99 מאמרים כאלה בספר הלימוד וניתן לפתוח מיד גישה לכל המשימות ולכל הטקסטים המוסתרים שבהם.
במקרה השני אנחנו ניתן לךסימולטור "6000 משימות עם פתרונות ותשובות, לכל נושא, לכל רמות המורכבות." זה בהחלט מספיק כדי לשים את ידך על פתרון בעיות בכל נושא.
למעשה, מדובר בהרבה יותר מסתם סימולטור – תוכנית אימונים שלמה. במידת הצורך, אתה יכול גם להשתמש בו בחינם.
גישה לכל הטקסטים והתכניות ניתנת למשך כל חיי האתר.
לסיכום...
אם אתה לא אוהב את המשימות שלנו, מצא אחרים. רק אל תפסיק עם התיאוריה.
"מובן" ו"אני יודע לפתור" הם כישורים שונים לחלוטין. אתה צריך את שניהם.
מצא בעיות ופתור!