הוכח שקו האמצע של הטרפז מקביל לבסיסים. קו חציון של הטרפז

מרובעים.

§ 49. TRAPEZIA.

מרובע שבו שתי צלעות מנוגדות מקבילות ושתי האחרות אינן מקבילות נקרא טרפז.

בשרטוט 252, המרובע ABDC AB || CD, AC || ב.ד. ABDC - טרפז.

הצלעות המקבילות של טרפז נקראות שלה עילה; AB ו-CD הם הבסיסים של הטרפז. שני הצדדים האחרים נקראים הצדדיםטרַפֵּז; AC ו-BD הם הצדדים של הטרפז.

אם הצלעות שוות, אזי נקרא טרפז שְׁוֵה שׁוֹקַיִם.

הטרפז ABOM הוא שווה שוקיים, שכן AM=BO (איור 253).

טרפז שבו אחת מהצלעות מאונך לבסיס נקרא מַלבֵּנִי(מפתח 254).

קו החציון של טרפז הוא קטע המחבר בין נקודות האמצע של צלעות הטרפז.

מִשׁפָּט. קו אמצעיטרפז מקביל לכל אחד מהבסיסים שלו ושווה לחצי הסכום שלהם.

נתון: OS - הקו האמצעי של טרפז ABDK, כלומר אישור \u003d OA ו-BC \u003d CD (איור 255).

עלינו להוכיח:

1) מערכת הפעלה || KD ומערכת ההפעלה || AB;
2)

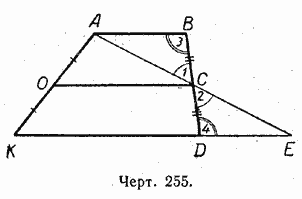
הוכחה.צייר קו דרך נקודות A ו-C שחותך את המשך הבסיס KD בנקודה E כלשהי.

במשולשים ABC ו-DCE:
BC \u003d CD - לפי תנאי;
/ 1 = / 2 כאנכי,
/ 4 = / 3, כמו פנימי מוצלב שוכב עם מקביל AB ו-KE ו-Secant BD. כתוצאה מכך, /\ ABC = /\ DSE.

לפיכך, AC = CE, כלומר. OS הוא קו האמצע של המשולש KAE. לפיכך (סעיף 48):

1) מערכת הפעלה || KE ולפיכך OS || KD ומערכת ההפעלה || AB;
2) , אבל DE \u003d AB (מהשוויון של משולשים ABC ו-DCE), כך שניתן להחליף את הקטע DE בקטע AB השווה לו. ואז נקבל:

המשפט הוכח.

תרגילים.

1. הוכח שסכום הזוויות הפנימיות של טרפז הצמוד לכל צד הוא 2 ד.

2. הוכיחו שהזוויות בבסיס טרפז שווה שוקיים שוות.

3. הוכיחו שאם הזוויות בבסיס הטרפז שוות, אז הטרפז הזה הוא שווה שוקיים.

4. הוכיחו שהאלכסונים של טרפז שווה שוקיים שווים זה לזה.

5. הוכיחו שאם האלכסונים של טרפז שווים, אז הטרפז הזה הוא שווה שוקיים.

6. הוכיחו שהיקף הדמות שנוצרה על ידי הקטעים המחברים את נקודות האמצע של צלעות המרובע הוא שווה לסכוםאלכסונים של מרובע זה.

7. הוכיחו שקו ישר העובר באמצע אחת מצלעות הטרפז המקבילות לבסיסיו מחלק את הצד השני של הטרפז לשניים.

הפרטיות שלך חשובה לנו. מסיבה זו, פיתחנו מדיניות פרטיות המתארת כיצד אנו משתמשים ומאחסנים את המידע שלך. אנא קרא את מדיניות הפרטיות שלנו ויידע אותנו אם יש לך שאלות כלשהן.

איסוף ושימוש במידע אישי

מידע אישי מתייחס לנתונים שניתן להשתמש בהם כדי לזהות או ליצור קשר עם אדם ספציפי.

ייתכן שתתבקש לספק את המידע האישי שלך בכל עת בעת יצירת קשר.

להלן מספר דוגמאות לסוגי המידע האישי שאנו עשויים לאסוף וכיצד אנו עשויים להשתמש במידע כזה.

איזה מידע אישי אנחנו אוספים:

בעת הגשת בקשה לאתר, אנו עשויים לאסוף פרטים שונים, לרבות שמך, מספר הטלפון, כתובתך אימיילוכו '

כיצד אנו משתמשים במידע האישי שלך:

המידע האישי שאנו אוספים מאפשר לנו ליצור איתך קשר וליידע אותך לגבי הצעות ייחודיות, מבצעים ואירועים אחרים ואירועים קרובים.
מעת לעת, אנו עשויים להשתמש במידע האישי שלך כדי לשלוח לך הודעות והודעות חשובות.
אנו עשויים להשתמש במידע אישי גם למטרות פנימיות, כגון ביצוע ביקורות, ניתוח נתונים ומחקרים שונים על מנת לשפר את השירותים שאנו מספקים ולספק לך המלצות לגבי השירותים שלנו.
אם תצטרף להגרלת פרס, לתחרות או תמריץ דומה, אנו עשויים להשתמש במידע שאתה מספק כדי לנהל תוכניות כאלה.

חשיפה לצדדים שלישיים

איננו חושפים מידע שהתקבל ממך לצדדים שלישיים.

חריגים:

במידת הצורך - בהתאם לחוק, צו שיפוטי, ב ליטיגציה, ו/או בהתבסס על בקשות ציבוריות או בקשות מ סוכנויות ממשלתיותבשטח הפדרציה הרוסית - לחשוף את המידע האישי שלך. אנו עשויים גם לחשוף מידע אודותיך אם נקבע כי חשיפה כזו היא הכרחית או מתאימה עבור אבטחה, אכיפת חוק או ציבור אחר אירועים חשובים.
במקרה של ארגון מחדש, מיזוג או מכירה, אנו עשויים להעביר את המידע האישי שאנו אוספים ליורש הצד השלישי הרלוונטי.

הגנה על מידע אישי

אנו נוקטים באמצעי זהירות - לרבות מנהליים, טכניים ופיסיים - כדי להגן על המידע האישי שלך מפני אובדן, גניבה ושימוש לרעה, כמו גם מפני גישה לא מורשית, חשיפה, שינוי והרס.

שמירה על פרטיותך ברמת החברה

כדי להבטיח שהמידע האישי שלך מאובטח, אנו מעבירים לעובדים שלנו נוהלי פרטיות ואבטחה ואוכפים בקפדנות את נוהלי הפרטיות.

\[(\Large(\text(טרפז שרירותי)))\]

הגדרות

טרפז הוא מרובע קמור בו שתי צלעות מקבילות ושתי צלעות אחרות אינן מקבילות.

הצלעות המקבילות של טרפז נקראות הבסיסים שלו, ושתי הצלעות האחרות נקראות הצלעות שלו.

גובהו של טרפז הוא האנך שנפל מכל נקודה של בסיס אחד לבסיס אחר.

משפטים: תכונות של טרפז

1) סכום הזוויות בצד הוא $180^\circ$ .

2) האלכסונים מחלקים את הטרפז לארבעה משולשים, שניים מהם דומים ושני האחרים שווים.

הוכחה

1) בגלל $AD\parallel BC$ , אזי הזוויות $\angle BAD$ ו-$\angle ABC$ חד-צדדיות בקווים אלה והחתך $AB$ , לכן, $\angle BAD +\angle ABC=180^\circ$.

2) כי $AD\parallel BC$ ו-$BD$ הוא סקאנט, ואז $\angle DBC=\angle BDA$ כמו שוכב לרוחב.
גם $\angle BOC=\angle AOD$ כאנכי.
לכן, בשתי פינות $\משולש BOC \sim \triangle AOD$.

בואו נוכיח את זה $S_(\triangle AOB)=S_(\triangle COD)$. תן $h$ להיות גובה הטרפז. לאחר מכן $S_(\triangle ABD)=\frac12\cdot h\cdot AD=S_(\triangle ACD)$. לאחר מכן: \

הַגדָרָה

קו האמצע של טרפז הוא קטע המחבר בין נקודות האמצע של הצדדים.

מִשׁפָּט

קו החציון של הטרפז מקביל לבסיסים ושווה למחצית הסכום שלהם.

הוכחה*

1) בואו נוכיח את ההקבלה.

צייר קו $MN"\מקביל AD$ ($N"\בתקליטור$ ) דרך הנקודה $M$ ). לאחר מכן, לפי משפט תאלס (כי $MN"\parallel AD\parallel BC, AM=MB$) הנקודה $N"$ היא נקודת האמצע של הקטע $CD$... לפיכך, הנקודות $N$ ו-$N"$ יחולפו.

2) בואו נוכיח את הנוסחה.

בואו נצייר $BB"\perp AD, CC"\perp AD$ . תן $BB"\cap MN=M", CC"\cap MN=N"$.

לאחר מכן, לפי משפט תאלס, $M"$ ו-$N"$ הם נקודות האמצע של המקטעים $BB"$ ו-$CC"$, בהתאמה. אז $MM"$ הוא הקו האמצעי $\משולש ABB"$ , $NN"$ הוא הקו האמצעי $\משולש DCC"$ . זו הסיבה: \

כי $MN\parallel AD\parallel BC$ו-$BB", CC"\perp AD$, אז $B"M"N"C"$ ו-$BM"N"C$ הם מלבנים. לפי משפט Thales, $MN\מקביל AD$ ו-$AM=MB$ מרמזים ש-$B"M"=M"B$ . לפיכך, $B"M"N"C"$ ו-$BM"N"C$ הם מלבנים שווים, ומכאן $M"N"=B"C"=BC$ .

בדרך זו:

\ \[=\dfrac12 \left(AB"+B"C"+BC+C"D\right)=\dfrac12\left(AD+BC\right)\]

משפט: תכונה של טרפז שרירותי

נקודות האמצע של הבסיסים, נקודת החיתוך של אלכסוני הטרפז ונקודת החיתוך של שלוחות הצדדים הרוחביים שוכנות על אותו קו ישר.

הוכחה*
מומלץ להכיר את ההוכחה לאחר לימוד הנושא "משולשים דומים".

1) הבה נוכיח שהנקודות $P$ , $N$ ו-$M$ שוכנות על אותו קו ישר.

צייר קו $PN$ ($P$ היא נקודת החיתוך של שלוחות הצלעות, $N$ היא נקודת האמצע של $BC$ ). תנו לו לחצות את הצלע $AD$ בנקודה $M$ . הבה נוכיח ש-$M$ היא נקודת האמצע של $AD$ .

שקול את $\משולש BPN$ ו-$\משולש APM$ . הם דומים בשתי זוויות ($\angle APM$ - משותף, $\angle PAM=\angle PBN$ כמתאים ב-$AD\parallel BC$ ו-$AB$ secant). אומר: \[\dfrac(BN)(AM)=\dfrac(PN)(PM)\]

שקול את $\triangle CPN$ ו-$\triangle DPM$ . הם דומים בשתי זוויות ($\angle DPM$ - משותף, $\angle PDM=\angle PCN$ כמתאימות ב-$AD\parallel BC$ ו-$CD$ secant). אומר: \[\dfrac(CN)(DM)=\dfrac(PN)(PM)\]

מכאן $\dfrac(BN)(AM)=\dfrac(CN)(DM)$. אבל $BN=NC$ , ומכאן $AM=DM$ .

2) הבה נוכיח שהנקודות $N, O, M$ שוכנות על קו ישר אחד.

תן $N$ להיות נקודת האמצע של $BC$ , $O$ להיות נקודת החיתוך של האלכסונים. צייר קו $NO$ , הוא יחצה את הצלע $AD$ בנקודה $M$ . הבה נוכיח ש-$M$ היא נקודת האמצע של $AD$ .

$\triangle BNO\sim \triangle DMO$בשתי זוויות ($\angle OBN=\angle ODM$ כמו מונח ב-$BC\parallel AD$ ו-$BD$ secant; $\angle BON=\angle DOM$ כאנכי). אומר: \[\dfrac(BN)(MD)=\dfrac(ON)(OM)\]

באופן דומה $\triangle CON\sim \triangle AOM$. אומר: \[\dfrac(CN)(MA)=\dfrac(ON)(OM)\]

מכאן $\dfrac(BN)(MD)=\dfrac(CN)(MA)$. אבל $BN=CN$ , ומכאן $AM=MD$ .

\[(\Large(\text(טרפז שווה שוקיים)))\]

הגדרות

טרפז נקרא מלבני אם אחת מהזוויות שלו ישרה.

טרפז נקרא שווה שוקיים אם צלעותיו שוות.

משפטים: תכונות של טרפז שווה שוקיים

1) לטרפז שווה שוקיים יש זוויות בסיס שוות.

2) האלכסונים של טרפז שווה שוקיים שווים.

3) שני המשולשים הנוצרים מהאלכסונים והבסיס הם שווה שוקיים.

הוכחה

1) קחו בחשבון טרפז שווה שוקיים $ABCD$ .

מהקודקודים $B$ ו-$C$ נשמט לצד $AD$ את הניצבים $BM$ ו-$CN$, בהתאמה. מאז $BM\perp AD$ ו-$CN\perp AD$ , אז $BM\parallel CN$ ; $AD\parallel BC$ , אז $MBCN$ היא מקבילית, ומכאן $BM = CN$ .

שקול משולשים ישרים $ABM$ ו-$CDN$ . מכיוון שיש להם תחתונים שווים והרגל $BM$ שווה לרגל $CN$ , משולשים אלה חופפים, לכן, $\angle DAB = \angle CDA$ .

כי $AB=CD, \angle A=\angle D, AD$- כללי, ואז על השלט הראשון. לכן, $AC=BD$ .

3) בגלל $\משולש ABD=\משולש ACD$, ואז $\angle BDA=\angle CAD$ . לכן, המשולש $\משולש AOD$ הוא שווה שוקיים. ניתן להוכיח באופן דומה ש-$\משולש BOC$ הוא שווה שוקיים.

משפטים: סימנים של טרפז שווה שוקיים

1) אם הזוויות בבסיס הטרפז שוות, אז הוא שווה שוקיים.

2) אם האלכסונים של טרפז שווים, אז הוא שווה שוקיים.

הוכחה

שקול טרפז $ABCD$ כך ש-$\angle A = \angle D$ .

הבה נשלים את הטרפז למשולש $AED$ כפי שמוצג באיור. מכיוון ש-$\angle 1 = \angle 2$ , אז המשולש $AED$ הוא שווה שוקיים ו-$AE = ED$ . הזוויות $1$ ו-$3$ שוות כמתאימות לקווים מקבילים $AD$ ו-$BC$ והחתך $AB$ . באופן דומה, הזוויות $2$ ו-$4$ שוות, אבל $\angle 1 = \angle 2$ , אז $\angle 3 = \angle 1 = \angle 2 = \angle 4$, לכן, המשולש $BEC$ הוא גם שווה שוקיים ו-$BE = EC$ .

בסופו של דבר $AB = AE - BE = DE - CE = CD$, כלומר $AB = CD$ , שהיה צריך להוכיח.

2) תן $AC=BD$ . כי $\triangle AOD\sim \triangle BOC$, אז נסמן את מקדם הדמיון שלהם ב-$k$ . ואז אם $BO=x$ , אז $OD=kx$ . בדומה ל-$CO=y \Rightarrow AO=ky$ .

כי $AC=BD$, ואז $x+kx=y+ky \Rightarrow x=y$ . אז $\משולש AOD$ הוא שווה שוקיים ו-$\angle OAD=\angle ODA$ .

כך, לפי הסימן הראשון $\משולש ABD=\משולש ACD$ ($AC=BD, \angle OAD=\angle ODA, AD$- כללי). אז $AB=CD$, אז.

איסוף ושימוש במידע אישי

מידע אישי מתייחס לנתונים שניתן להשתמש בהם כדי לזהות או ליצור קשר עם אדם ספציפי.

ייתכן שתתבקש לספק את המידע האישי שלך בכל עת בעת יצירת קשר.

להלן מספר דוגמאות לסוגי המידע האישי שאנו עשויים לאסוף וכיצד אנו עשויים להשתמש במידע כזה.

איזה מידע אישי אנחנו אוספים:

בעת הגשת בקשה לאתר, אנו עשויים לאסוף פרטים שונים, לרבות שמך, מספר הטלפון, כתובת הדואר האלקטרוני שלך וכו'.

כיצד אנו משתמשים במידע האישי שלך:

המידע האישי שאנו אוספים מאפשר לנו ליצור איתך קשר וליידע אותך לגבי הצעות ייחודיות, מבצעים ואירועים נוספים ואירועים קרובים.
מעת לעת, אנו עשויים להשתמש במידע האישי שלך כדי לשלוח לך הודעות והודעות חשובות.
אנו עשויים להשתמש במידע אישי גם למטרות פנימיות, כגון ביצוע ביקורות, ניתוח נתונים ומחקרים שונים על מנת לשפר את השירותים שאנו מספקים ולספק לך המלצות לגבי השירותים שלנו.
אם תצטרף להגרלת פרס, לתחרות או תמריץ דומה, אנו עשויים להשתמש במידע שאתה מספק כדי לנהל תוכניות כאלה.

חשיפה לצדדים שלישיים

איננו חושפים מידע שהתקבל ממך לצדדים שלישיים.

חריגים:

במקרה שהדבר נחוץ - בהתאם לחוק, לצו שיפוטי, בהליכים משפטיים ו/או בהתבסס על בקשות או בקשות ציבוריות מגופים ממלכתיים בשטח הפדרציה הרוסית - חשפו את המידע האישי שלכם. אנו עשויים גם לחשוף מידע אודותיך אם נקבע כי חשיפה כזו נחוצה או מתאימה מסיבות אבטחה, אכיפת חוק או אינטרס ציבורי אחר.
במקרה של ארגון מחדש, מיזוג או מכירה, אנו עשויים להעביר את המידע האישי שאנו אוספים ליורש הצד השלישי הרלוונטי.

הגנה על מידע אישי

שמירה על פרטיותך ברמת החברה

הרעיון של קו האמצע של הטרפז

ראשית, בואו נזכור איזו דמות נקראת טרפז.

הגדרה 1

טרפז הוא מרובע שבו שתי צלעות מקבילות ושתי האחרות אינן מקבילות.

במקרה זה, צלעות מקבילות נקראות בסיסי הטרפז, ולא מקבילות - צלעות הטרפז.

הגדרה 2

קו האמצע של טרפז הוא קטע קו המחבר בין נקודות האמצע של צלעות הטרפז.

משפט קו האמצע של טרפז

כעת אנו מציגים את המשפט על קו האמצע של טרפז ומוכיחים אותו בשיטת הווקטור.

משפט 1

קו החציון של הטרפז מקביל לבסיסים ושווה למחצית הסכום שלהם.

הוכחה.

הבה ניתן לנו טרפז $ABCD$ עם בסיסים $AD\ ו\BC$. ותן $MN$ להיות קו האמצע של הטרפז הזה (איור 1).

איור 1. הקו האמצעי של הטרפז

הבה נוכיח ש$MN||AD\ and\ MN=\frac(AD+BC)(2)$.

שקול את הווקטור $\overrightarrow(MN)$. לאחר מכן, אנו משתמשים בכלל המצולע לחיבור וקטור. מצד אחד, אנחנו מבינים את זה

מצד שני

אם נוסיף את שני השוויון האחרונים, נקבל

מכיוון ש-$M$ ו-$N$ הם נקודות האמצע של צלעות הטרפז, יש לנו

אנחנו מקבלים:

כתוצאה מכך

מאותו שוויון (מכיוון ש$\overrightarrow(BC)$ ו-$\overrightarrow(AD)$ הם קו-כיווני, ולכן, קולינאריים), אנו מקבלים את $MN||AD$.

המשפט הוכח.

דוגמאות למשימות על מושג קו האמצע של טרפז

דוגמה 1

הצדדים של הטרפז הם $15\cm$ ו-$17\cm$ בהתאמה. היקף הטרפז הוא $52\cm$. מצא את אורך קו האמצע של הטרפז.

פִּתָרוֹן.

סמן את קו האמצע של הטרפז ב-$n$.

סכום הצלעות הוא

לכן, מכיוון שההיקף הוא $52\ ס"מ$, סכום הבסיסים הוא

לפיכך, לפי משפט 1, אנו מקבלים

תשובה:$10\ס"מ$.

דוגמה 2

קצוות קוטר המעגל הם $9$ ס"מ ו-$5$ ס"מ בהתאמה מהמשיק שלו. מצאו את קוטר המעגל הזה.

פִּתָרוֹן.

תנו לנו מעגל עם מרכז $O$ ובקוטר $AB$. צייר את המשיק $l$ ובנה את המרחקים $AD=9\ cm$ ו-$BC=5\ cm$. נצייר את הרדיוס $OH$ (איור 2).

איור 2.

מכיוון ש$AD$ ו-$BC$ הם המרחקים למשיק, אז $AD\bot l$ ו-$BC\bot l$ ומכיוון ש$OH$ הוא הרדיוס, אז $OH\bot l$, ומכאן $OH | \left|AD\right||BC$. מכל זה אנו מבינים ש$ABCD$ הוא טרפז, ו-$OH$ הוא קו האמצע שלו. לפי משפט 1, אנחנו מקבלים