הגדלה של הגרף. הגדלה והקטנה של הפונקציה במרווח, אקסטרים

עבודת סיום בצורת בחינת המדינה המאוחדת לתלמידי כיתות י"א מכילה בהכרח משימות לחישוב הגבולות, מרווחי הקטנה והגדלת הנגזרת של פונקציה, מציאת נקודות קיצון ושרטוט גרפים. ידע טובנושא זה מאפשר לך לענות נכון על מספר שאלות של הבחינה ולא לחוות קשיים בהכשרה מקצועית נוספת.

יסודות החשבון הדיפרנציאלי הוא אחד הנושאים העיקריים של המתמטיקה של בית הספר המודרני. היא חוקרת את השימוש בנגזרת כדי לחקור את התלות של משתנים – באמצעות הנגזרת ניתן לנתח את העלייה והירידה של פונקציה מבלי להתייחס לשרטוט.

הכנה מקיפה של בוגרים ל-USE עבור פורטל חינוכי"שקולקובו" יעזור להבין לעומק את עקרונות הבידול - להבין את התיאוריה בפירוט, ללמוד דוגמאות לפתרון בעיות אופייניות ולנסות את כוחך בעבודה עצמאית. אנו נעזור לך לבטל פערים בידע - כדי להבהיר את הבנתך את המושגים המילוניים של הנושא ואת התלות בכמויות. התלמידים יוכלו לחזור על איך למצוא מרווחים של מונוטוניות, כלומר עלייה או ירידה של הנגזרת של פונקציה על מרווח מסוים, כאשר נקודות הגבול כלולות ולא נכללות במרווחים שנמצאו.

לפני שמתחילים בפתרון ישיר של בעיות נושאיות, אנו ממליצים לעבור תחילה לסעיף "התייחסות תיאורטית" ולחזור על הגדרות המושגים, הכללים והנוסחאות הטבלה. כאן תוכל גם לקרוא כיצד למצוא ולתעד כל מרווח של פונקציות גדלות ויורדות בגרף הנגזרת.

כל המידע המוצע מוצג בצורה הנגישה ביותר להבנה מעשית מאפס. האתר מספק חומרים לתפיסה והטמעה במספר צורות שונות– קריאה, צפייה בווידאו והדרכה ישירה בהדרכת מורים מנוסים. מחנכים מקצועייםהם יגידו לך בפירוט כיצד למצוא את מרווחי העלייה והירידה של הנגזרת של פונקציה באמצעות שיטות אנליטיות וגרפיות. במהלך הוובינרים ניתן יהיה לשאול כל שאלה שמעניינת הן בתיאוריה והן בפתרון בעיות ספציפיות.

לזכור את עיקרי הנושא, עיין בדוגמאות להגדלת הנגזרת של פונקציה, בדומה למשימות של אפשרויות הבחינה. כדי לגבש את מה שלמדת, עיין ב"קטלוג" - כאן תמצא תרגילים מעשייםל עבודה עצמאית. המשימות במדור נבחרות ברמות שונות של מורכבות, תוך התחשבות בפיתוח המיומנויות. לכל אחד מהם, למשל, מצורפים אלגוריתמי פתרון ותשובות נכונות.

על ידי בחירה בקטע קונסטרוקטור, התלמידים יוכלו להתאמן בחקירת העלייה והירידה של הנגזרת של פונקציה ב- אפשרויות אמיתיותבחינת מדינה מאוחדת, מתעדכנת כל הזמן תוך התחשבות שינויים אחרוניםוחדשנות.

מאוד מידע חשובעל התנהגות הפונקציה לספק טווחים של עלייה ויורדת. מציאתם היא חלק מתהליך חקר הפונקציות והזימה. בנוסף, ניתנות נקודות הקיצון, בהן יש שינוי מעלייה לירידה או מירידה לעלייה תשומת - לב מיוחדתכאשר מוצאים את הערך הגדול והקטן ביותר של פונקציה במרווח מסוים.

במאמר זה, אנו נותנים את ההגדרות הדרושות, מנסחים סימן מספיקהגדלה והקטנה של פונקציה על מרווח ותנאים מספיקים לקיומו של קיצון, אנו מיישמים את כל התיאוריה הזו לפתרון דוגמאות ובעיות.

ניווט בדף.

הגדלת והקטנת תפקוד על מרווח.

הגדרה של פונקציה גוברת.

הפונקציה y=f(x) גדלה במרווח X אם עבור כל ו אי השוויון מרוצה. במילים אחרות - ערך גדול יותרהארגומנט מתאים לערך הגדול יותר של הפונקציה.

הגדרת פונקציה יורדת.

הפונקציה y=f(x) יורדת במרווח X אם עבור כל ו את אי השוויון . במילים אחרות, ערך גדול יותר של הארגומנט מתאים לערך קטן יותר של הפונקציה.

הערה: אם הפונקציה מוגדרת ורציפה בקצוות מרווח העלייה או הירידה (a;b), כלומר ב-x=a ו-x=b, אז נקודות אלו נכללות במרווח העלייה או הירידה. זה לא סותר את ההגדרות של פונקציה עולה ויורדת במרווח X.

לדוגמה, מהמאפיינים של הפונקציות היסודיות הבסיסיות, אנו יודעים ש-y=sinx מוגדר ורציף עבור כל הערכים האמיתיים של הארגומנט. לכן, מהגדלת פונקציית הסינוס במרווח, נוכל לקבוע את העלייה במרווח .

נקודות קיצון, פונקציה אקסטרים.

הנקודה נקראת נקודת מקסימוםפונקציה y=f(x) אם אי השוויון נכון עבור כל x מהשכונה שלו. הערך של הפונקציה בנקודת המקסימום נקרא לתפקד מקסימוםוסמן .

הנקודה נקראת נקודת מינימוםפונקציה y=f(x) אם אי השוויון נכון עבור כל x מהשכונה שלו. הערך של הפונקציה בנקודת המינימום נקרא מינימום פונקציהוסמן .

השכונה של נקודה מובנת כמרווח , היכן הוא מספר חיובי קטן מספיק.

נקודות המינימום והמקסימום נקראות נקודות קיצון, וערכי הפונקציה התואמים לנקודות הקיצון נקראים תפקוד אקסטרים.

אין לבלבל בין קיצוניות של פונקציה לבין ערכי המקסימום והמינימום של הפונקציה.

באיור הראשון מגיעים לערך המקסימלי של הפונקציה על הקטע בנקודת המקסימום והוא שווה למקסימום של הפונקציה, ובאיור השני מגיעים לערך המקסימלי של הפונקציה בנקודה x=b , שאינה נקודת המקסימום.

תנאים מספיקים להגדלת והקטנת פונקציות.

על בסיס תנאים מספיקים (סימנים) לעלייה וירידה של התפקוד, מוצאים את מרווחי העלייה והירידה של התפקוד.

להלן הניסוחים של הסימנים של עלייה וירידה בפונקציות במרווח:

• אם הנגזרת של הפונקציה y=f(x) חיובית עבור כל x מהמרווח X, אז הפונקציה גדלה ב-X;
• אם הנגזרת של הפונקציה y=f(x) שלילית עבור כל x מהמרווח X, אז הפונקציה יורדת ב-X.

לפיכך, כדי לקבוע את מרווחי העלייה והירידה של פונקציה, יש צורך:

שקול דוגמה למציאת המרווחים של פונקציות הגדלות והקטנות כדי להבהיר את האלגוריתם.

דוגמא.

מצא את מרווחי העלייה והירידה של הפונקציה.

פִּתָרוֹן.

הצעד הראשון הוא למצוא את היקף הפונקציה. בדוגמה שלנו, הביטוי במכנה לא צריך להיעלם, לכן, .

נעבור למציאת הנגזרת של הפונקציה:

כדי לקבוע את מרווחי העלייה והירידה של פונקציה לפי קריטריון מספיק, אנו פותרים את אי השוויון ובתחום ההגדרה. הבה נשתמש בהכללה של שיטת המרווחים. השורש האמיתי היחיד של המונה הוא x = 2, והמכנה נעלם ב-x=0. נקודות אלו מחלקות את תחום ההגדרה למרווחים שבהם הנגזרת של הפונקציה שומרת על הסימן שלה. נסמן את הנקודות הללו על קו המספרים. באמצעות פלוסים ומינוסים, אנו מציינים באופן מותנה את המרווחים שבהם הנגזרת חיובית או שלילית. החצים למטה מציגים באופן סכמטי את העלייה או הירידה של הפונקציה במרווח המתאים.

לכן, ו .

בנקודה x=2 הפונקציה מוגדרת ורציפה, ולכן יש להוסיף אותה גם למרווחים העולה וגם בירידה. בנקודה x=0, הפונקציה אינה מוגדרת, ולכן נקודה זו אינה כלולה במרווחים הנדרשים.

אנו מציגים את הגרף של הפונקציה כדי להשוות את התוצאות שהתקבלו איתה.

תשובה:

הפונקציה גדלה בשעה , יורד במרווח (0;2] .

תנאים מספיקים לקיצוניות של פונקציה.

כדי למצוא את המקסימום והמינימום של פונקציה, ניתן להשתמש בכל אחד משלושת סימני הקיצון, כמובן, אם הפונקציה עומדת בתנאים שלהם. הנפוץ והנוח ביותר הוא הראשון שבהם.

התנאי הראשון המספיק לקיצוניות.

תנו לפונקציה y=f(x) להיות ניתנת להבדלה ב- -שכונה של הנקודה ולהיות רציפה בנקודה עצמה.

במילים אחרות:

אלגוריתם למציאת נקודות קיצון לפי הסימן הראשון של הפונקציה קיצונית.

• מציאת היקף הפונקציה.
• אנו מוצאים את הנגזרת של הפונקציה בתחום ההגדרה.
• אנו קובעים את האפסים של המונה, את האפסים של המכנה של הנגזרת ואת הנקודות של התחום שבו הנגזרת לא קיימת (כל הנקודות הרשומות נקראות נקודות קיצון אפשריות, עובר דרך נקודות אלה, הנגזרת פשוט יכולה לשנות את הסימן שלה).
• נקודות אלו מחלקות את תחום הפונקציה למרווחים שבהם הנגזרת שומרת על הסימן שלה. אנו קובעים את הסימנים של הנגזרת בכל אחד מהמרווחים (לדוגמה, על ידי חישוב הערך של הנגזרת של הפונקציה בכל נקודה של מרווח בודד).
• אנו בוחרים נקודות שבהן הפונקציה רציפה ובמעבר דרכן, הנגזרת משנה סימן - הן נקודות הקיצון.

יותר מדי מילים, הבה נבחן כמה דוגמאות למציאת נקודות קיצון ונקודות קיצון של פונקציה באמצעות התנאי הראשון המספיק לקיצון של פונקציה.

דוגמא.

מצא את הקיצוניות של הפונקציה.

פִּתָרוֹן.

היקף הפונקציה הוא כל קבוצת המספרים הממשיים, למעט x=2 .

אנו מוצאים את הנגזרת:

האפסים של המונה הם הנקודות x=-1 ו-x=5, המכנה הולך לאפס ב-x=2. סמן את הנקודות הללו על קו המספרים

אנו קובעים את הסימנים של הנגזרת בכל מרווח, לשם כך אנו מחשבים את ערך הנגזרת בכל אחת מהנקודות של כל מרווח, למשל, בנקודות x=-2, x=0, x=3 ו-x= 6 .

לכן, הנגזרת חיובית על המרווח (בתמונה שמנו סימן פלוס על המרווח הזה). באופן דומה

לכן, שמנו מינוס על המרווח השני, מינוס על השלישי ופלוס על הרביעי.

נותר לבחור את הנקודות בהן הפונקציה רציפה והנגזרת שלה משנה סימן. אלו נקודות הקיצון.

בנקודה x=-1 הפונקציה היא רציפה והנגזרת משנה סימן מפלוס למינוס, לכן, לפי הסימן הראשון של הקיצון, x=-1 היא נקודת המקסימום, היא תואמת למקסימום של הפונקציה .

בנקודה x=5 הפונקציה רציפה והנגזרת משנה סימן מינוס לפלוס, לכן, x=-1 היא נקודת המינימום, היא מתאימה למינימום של הפונקציה .

איור גרפי.

תשובה:

שימו לב: הסימן הראשון המספיק של קיצון אינו מחייב את הפונקציה להיות ניתנת להבדלה בנקודה עצמה.

דוגמא.

מצא נקודות קיצון וקיצוניות של פונקציה .

פִּתָרוֹן.

תחום הפונקציה הוא כל קבוצת המספרים הממשיים. ניתן לכתוב את הפונקציה עצמה כך:

בוא נמצא את הנגזרת של הפונקציה:

בנקודה x=0 הנגזרת אינה קיימת, מכיוון שהערכים של מגבלות חד-צדדיות אינם חופפים כאשר הארגומנט שואף לאפס:

יחד עם זאת, הפונקציה המקורית היא רציפה בנקודה x=0 (ראה סעיף על חקירת פונקציה להמשכיות):

מצא את הערכים של הארגומנט שבו הנגזרת נעלמת:

אנו מסמנים את כל הנקודות שהתקבלו על הישר האמיתי וקובעים את הסימן של הנגזרת בכל אחד מהמרווחים. לשם כך, אנו מחשבים את ערכי הנגזרת בנקודות שרירותיות של כל מרווח, למשל, כאשר x=-6, x=-4, x=-1, x=1, x=4, x=6.

זה,

לפיכך, לפי הסימן הראשון של קיצון, נקודות המינימום הן , הנקודות המקסימליות הן .

אנו מחשבים את המינימום התואם של הפונקציה

אנו מחשבים את המקסימום התואם של הפונקציה

איור גרפי.

תשובה:

.

הסימן השני לקיצוני הפונקציה.

כפי שאתה יכול לראות, סימן זה של הקיצון של הפונקציה מחייב קיום של נגזרת לפחות עד הסדר השני בנקודה .

פונקציות קיצוניות

הגדרה 2

נקודה $x_0$ נקראת נקודת מקסימום של הפונקציה $f(x)$ אם קיימת שכונה של נקודה זו כך שלכל $x$ משכונה זו האי-שוויון $f(x)\le f(x_0 )$ מרוצה.

הגדרה 3

נקודה $x_0$ נקראת נקודת מקסימום של הפונקציה $f(x)$ אם קיימת שכונה של נקודה זו כך שלכל $x$ משכונה זו האי-שוויון $f(x)\ge f(x_0) $ מרוצה.

המושג קיצון של פונקציה קשור קשר הדוק למושג נקודה קריטית של פונקציה. הבה נציג את ההגדרה שלו.

הגדרה 4

$x_0$ נקרא נקודה קריטית של הפונקציה $f(x)$ אם:

1) $x_0$ - נקודה פנימית של תחום ההגדרה;

2) $f"\left(x_0\right)=0$ או לא קיים.

למושג קיצון אפשר לנסח משפטים על תנאים מספיקים והכרחיים לקיומו.

משפט 2

מצב קיצוני מספיק

תן לנקודה $x_0$ להיות קריטית עבור הפונקציה $y=f(x)$ ושוכב במרווח $(a,b)$. הניחו בכל מרווח $\left(a,x_0\right)\ ו\ (x_0,b)$ הנגזרת $f"(x)$ קיימת ושמרו על סימן קבוע. לאחר מכן:

1) אם במרווח $(a,x_0)$ הנגזרת $f"\left(x\right)>0$, ובמרווח $(x_0,b)$ הנגזרת $f"\left(x\ ימין)

2) אם הנגזרת $f"\left(x\right)0$ נמצאת במרווח $(a,x_0)$, אז הנקודה $x_0$ היא נקודת המינימום עבור פונקציה זו.

3) אם גם במרווח $(a,x_0)$ וגם במרווח $(x_0,b)$ הנגזרת $f"\left(x\right) >0$ או הנגזרת $f"\left(x \ימין)

משפט זה מודגם באיור 1.

איור 1. תנאי מספיק לקיומה של אקסטרים

דוגמאות לקיצוניות (איור 2).

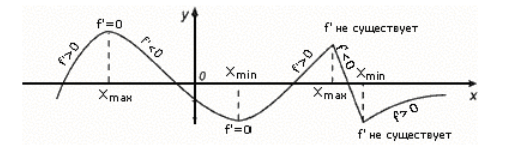
איור 2. דוגמאות לנקודות קיצון

הכלל לבחינת פונקציה לקיצון

2) מצא את הנגזרת $f"(x)$;

7) הסיק מסקנות לגבי נוכחות מקסימום ומינימום בכל מרווח, באמצעות משפט 2.

פונקציה עולה ויורדת

הבה נציג תחילה את ההגדרות של פונקציות הגדלות והקטנות.

הגדרה 5

פונקציה $y=f(x)$ המוגדרת במרווח $X$ נקראת הגדלה אם עבור נקודות כלשהן $x_1,x_2\in X$ עבור $x_1

הגדרה 6

פונקציה $y=f(x)$ המוגדרת במרווח $X$ נקראת הקטנה אם עבור נקודות כלשהן $x_1,x_2\in X$ עבור $x_1f(x_2)$.

בחינת פונקציה להגדלה והפחתה

אתה יכול לחקור פונקציות להגדלה והקטנה באמצעות הנגזרת.

על מנת לבחון פונקציה עבור מרווחי עלייה וירידה, עליך לבצע את הפעולות הבאות:

1) מצא את התחום של הפונקציה $f(x)$;

2) מצא את הנגזרת $f"(x)$;

3) מצא את הנקודות שבהן השוויון $f"\left(x\right)=0$;

4) מצא נקודות שבהן $f"(x)$ אינו קיים;

5) סמן על קו הקואורדינטות את כל הנקודות שנמצאו ואת התחום של הפונקציה הנתונה;

6) קבע את הסימן של הנגזרת $f"(x)$ בכל מרווח שמתקבל;

7) סיכמו: במרווחים שבהם $f"\left(x\right)0$ הפונקציה גדלה.

דוגמאות לבעיות לחקר פונקציות להגדלה, ירידה ונוכחות של נקודות קיצון

דוגמה 1

חקור את הפונקציה להגדלה והקטנה, ואת נוכחותן של נקודות מקסימום ומינימום: $f(x)=(2x)^3-15x^2+36x+1$

מכיוון ש-6 הנקודות הראשונות זהות, נצייר אותן תחילה.

1) תחום ההגדרה - כל המספרים הממשיים;

2) $f"\left(x\right)=6x^2-30x+36$;

3) $f"\left(x\right)=0$;

\ \ \

4) $f"(x)$ קיים בכל הנקודות של תחום ההגדרה;

5) קו קואורדינטות:

איור 3

6) קבע את הסימן של הנגזרת $f"(x)$ בכל מרווח:

\ \; .

הבה נקבע את הסימן של ערכי הפונקציה בקצות הקטע.

ו(0) = 3, ו(0) > 0

ו(10) = , ו(10) < 0.

מכיוון שהפונקציה יורדת בקטע והסימן של ערכי הפונקציה משתנה, אז יש אפס אחד של הפונקציה בקטע הזה.

תשובה: הפונקציה f(x) גדלה במרווחים: (-∞; 0]; ;

במרווח, לפונקציה יש אפס אחד מהפונקציה.

2. נקודות קיצון של הפונקציה: נקודות מקסימום ונקודות מינימום. תנאים הכרחיים ומספיקים לקיומו של קיצון של פונקציה. הכלל לבחינת פונקציה לקיצון .

הגדרה 1:הנקודות שבהן הנגזרת שווה לאפס נקראות קריטיות או נייחות.

הגדרה 2. נקודה נקראת נקודת מינימום (מקסימום) של הפונקציה אם ערך הפונקציה בנקודה זו קטן (גדול) מהערכים הקרובים ביותר של הפונקציה.

יש לזכור כי המקסימום והמינימום במקרה זה הם מקומיים.

על איור. 1. מתאר מקסימום ומינימום מקומיים.

המקסימום והמינימום של פונקציה מאוחדים בשם נפוץ: הקיצון של פונקציה.

משפט 1.(קריטריון הכרחי לקיומו של קיצון של הפונקציה). אם לפונקציה שניתן להבדיל בנקודה יש ​​מקסימום או מינימום בנקודה זו, אז הנגזרת שלה נעלמת ב-, .

משפט 2.(קריטריון מספיק לקיומו של קיצון של הפונקציה). אם לפונקציה רציפה יש נגזרת בכל הנקודות של מרווח כלשהו המכילה נקודה קריטית (למעט אולי נקודה זו עצמה), וכן אם הנגזרת, כאשר הארגומנט עובר משמאל לימין דרך הנקודה הקריטית, משנה סימן מפלוס למינוס, אז לפונקציה בנקודה זו יש מקסימום, וכאשר הסימן משתנה ממינוס לפלוס, יש לה מינימום.

נגזר. אם הנגזרת של פונקציה חיובית עבור כל נקודה במרווח, אז הפונקציה גדלה; אם היא שלילית, היא הולכת ופוחתת.

כדי למצוא את מרווחי העלייה והירידה של פונקציה, עליך למצוא את תחום ההגדרה שלה, הנגזרת, לפתור אי-שוויון בצורה F'(x) > 0 ו-F'(x)

פִּתָרוֹן.

3. לפתור את אי השוויון y' > 0 ו-y' 0;
(4 - x)/x³

פִּתָרוֹן.
1. מצא את התחום של הפונקציה. ברור שהביטוי במכנה חייב להיות תמיד שונה מאפס. לכן, 0 אינו נכלל מתחום ההגדרה: הפונקציה מוגדרת עבור x ∈ (-∞; 0)∪(0; +∞).

2. חשב את הנגזרת של הפונקציה:
y'(x) = ((3 x² + 2 x - 4)' x² – (3 x² + 2 x - 4) (x²)')/x^4 = ((6 x + 2) x² - (3 x²) + 2 x - 4) 2 x) / x^4 = (6 x³ + 2 x² - 6 x³ - 4 x² + 8 x) / x^ 4 \u003d (8 x - 2 x²) / x ^ 4 \u003d 2 (4 - x) / x³.

3. לפתור את אי השוויון y' > 0 ו-y' 0;
(4 - x)/x³

4. צד שמאללאי-שוויון יש x אמיתי אחד = 4 והוא הופך ל-x = 0. לכן, הערך x = 4 נכלל במרווח ובמרווח של ירידה, והנקודה 0 אינה נכללת.
אז, הפונקציה הנדרשת גדלה במרווח x ∈ (-∞; 0) ∪ .

4. בצד שמאל של אי השוויון יש x אמיתי אחד = 4 והוא הופך ב-x = 0. לכן, הערך x = 4 נכלל במרווח ובמרווח של ירידה, והנקודה 0 אינה נכללת.
אז, הפונקציה הנדרשת גדלה במרווח x ∈ (-∞; 0) ∪ .

מקורות:

• כיצד למצוא מרווחים יורדים בפונקציה

הפונקציה היא תלות קפדנית של מספר אחד במספר אחר, או הערך של הפונקציה (y) בארגומנט (x). ניתן לתאר כל תהליך (לא רק במתמטיקה) לפי תפקידו, שיהיו לו מאפיינים אופייניים: מרווחי ירידה ועלייה, נקודות של מינימה ומקסימום וכו'.

אתה תצטרך

• - עיתון;
• - עט.

הוראה

דוגמה 2
מצא את המרווחים של הפחתת f(x)=sinx +x.
הנגזרת של פונקציה זו תהיה שווה ל: f'(x)=cosx+1.
פתרון אי השוויון cosx+1

הַפסָקָה מוֹנוֹטוֹנִיוּתאפשר לקרוא לפונקציה מרווח שבו הפונקציה רק ​​גדלה או רק יורדת. מספר פעולות ספציפיות יעזרו למצוא טווחים כאלה עבור פונקציה, מה שנדרש לרוב בבעיות אלגבריות מסוג זה.

הוראה

השלב הראשון בפתרון הבעיה של קביעת המרווחים שבהם הפונקציה גדלה או יורדת באופן מונוטוני הוא חישוב הפונקציה הזו. כדי לעשות זאת, גלה את כל הערכים של הארגומנטים (ערכים על ציר ה-x) שעבורם אתה יכול למצוא את ערך הפונקציה. סמן את הנקודות בהן נצפים הפערים. מצא את הנגזרת של הפונקציה. לאחר הגדרת הביטוי המייצג את הנגזרת, השווה אותו לאפס. לאחר מכן, אתה צריך למצוא את השורשים של המתקבל. לא על השטח של ברזל.

הנקודות שבהן הפונקציה או שבהן הנגזרת שלה שווה לאפס הן גבולות המרווחים מוֹנוֹטוֹנִיוּת. טווחים אלה, כמו גם הנקודות המפרידות ביניהם, יש להזין בטבלה ברצף. מצא את הסימן של הנגזרת של הפונקציה במרווחים המתקבלים. לשם כך, החלף ארגומנט כלשהו מהמרווח בביטוי המתאים לנגזרת. אם התוצאה חיובית, הפונקציה בטווח זה גדלה, אחרת היא פוחתת. התוצאות מוזנות לטבלה.

השורה המציינת את הנגזרת של הפונקציה f'(x) נכתבת בהתאם לערכי הארגומנטים: "+" - אם הנגזרת חיובית, "-" - שלילית או "0" - שווה לאפס. בשורה הבאה, שימו לב למונוטוניות של הביטוי המקורי עצמו. החץ למעלה מתאים לעלייה, החץ למטה מתאים לירידה. בדוק את התכונות. אלו הן הנקודות שבהן הנגזרת היא אפס. נקודת קיצון יכולה להיות נקודה גבוהה או נקודה נמוכה. אם החלק הקודם של הפונקציה גדל, והנוכחי יורד, זו נקודת המקסימום. במקרה שבו הפונקציה הייתה יורדת עד לנקודה נתונה, ועכשיו היא גדלה, זו נקודת המינימום. הזינו בטבלה את ערכי הפונקציה בנקודות הקיצון.

מקורות:

• מהי ההגדרה של מונוטוניות

חקר ההתנהגות של פונקציה שיש לה תלות מורכבת בטיעון מתבצע באמצעות הנגזרת. לפי אופי השינוי בנגזרת, ניתן למצוא נקודות קריטיות ואזורי צמיחה או ירידה של הפונקציה.